搜索
【题目】小明利用灯光下自己的影子长度来测量路灯的高度．如图，CD和EF是两等高的路灯，相距27m，身高1.5m的小明（AB）站在两路灯之间（D、B、F共线），被两路灯同时照射留在地面的影长BQ=4m，BP=5m．
（1）小明距离路灯多远？
（2）求路灯高度．
参考答案：
【答案】
（1）
解答：设DB=xm，
∵AB∥CD，
∴∠QBA=∠QDC，∠QAB=∠QCD，
∴△QAB∽△QCD
∴ 
同理可得 
∵CD=EF
∴ 
∴ 
∴x=12
即小明距离路灯12m．
（2）
由 得 
∴CD=6
即路灯高6m．
【解析】先由已知条件得△QAB∽△QCD ， 列出比例式 ，同理可得 ，根据CD=EF ， 把相关数值代入可得小明距离路灯多远；第二题根据第一题得到的比例式及数值，计算可得路灯高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学兴趣小组的小明想测量教学楼前的一棵树的高度．下午课外活动时他测得一根长为1m的竹竿的影长是0.8m．但当他马上测量树高时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图）．他先测得留在墙壁上的树影高为1.2m，又测得地面的影长为2.6m，请你帮他算一下，下列哪个数字最接近树高（ ）m．
A.3.04
B.4.45
C.4.75
D.3.8 -
科目： 来源： 题型：
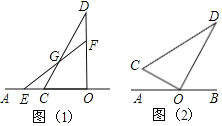
查看答案和解析>>【题目】如图，已知点O在直线AB上，将一副直角三角板的直角顶点放在点O处，其中∠OCD=60°，∠OEF=45°．边OC、OE在直线AB上．
（1）如图（1），若CD和EF相交于点G，则∠DGF的度数是______°；
（2）将图（1）中的三角板OCD绕点O顺时针旋转30°至图（2）位置
①若将三角板OEF绕点O顺时针旋转180°，在此过程中，当∠COE=∠EOD=∠DOF时，求∠AOE的度数；
②若将三角板OEF绕点O以每秒4°的速度顺时针旋转180°，与此同时，将三角板OCD绕点O以每秒1°的速度顺时针旋转，当三角板OEF旋转到终点位置时，三角板OCD也停止旋转．设旋转时间为t秒，当OD⊥EF时，求t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，∠A=90°，AB=AC ， BC=63cm，现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图所示，已知剪得的纸条中有一张是正方形，则这张正方形纸条是从下往上数第张．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C是直线AB，DE之间的一点，∠ACD=90°，下列条件能使得AB∥DE的是（ ）
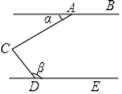
A. ∠α+∠β=180° B. ∠β﹣∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列条件中，能判定两个等腰三角形相似的是（ ）
A.都含有一个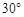
的内角
B.都含有一个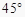
的内角
C.都含有一个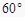
的内角
D.都含有一个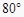
的内角 -
科目： 来源： 题型：
查看答案和解析>>【题目】某检修小组从A地出发，在东西方向的公路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶，纪录如下（单位：km）
第1次
第2次
第3次
第4次
第5次
第6次
第7次
﹣4
+7
﹣9
+8
+6
﹣5
﹣2
则收工时距A地多远？在第几次纪录时距A地最远？
A. 2千米 第1次 B. 1千米 第2次
C. 2千米 第4次 D. 1千米 第5次
相关试题
