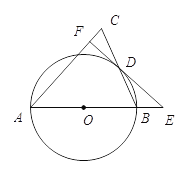
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,CD=BD,过点D作⊙O的切线交边AC于点F,交AB的延长线于点E.
(1)求证:EF⊥AC;
(2)若AF=9,EF=12,求OE的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OD,由切线的性质可得OD⊥DF,再利用圆周角定理证明AD⊥BC,根据等腰三角形的性质可证明OD∥AC,由平行线的性质即可得到EF⊥AC;
(2)首先根据勾股定理求出AE的长度,由OD∥AC,可得:△ODE∽△AEF,根据相似三角形的性质:对应边的比值相等即可得到关于OE的比例式,求出OE的值即可.
试题解析:
(1)证明:连接OD,如图所示.
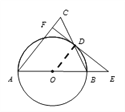
∵DF是⊙O的切线,D为切点,
∴OD⊥DF,
∴∠ODF=90°.
∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠CFD=∠ODF=90°,
∴EF⊥AC.
(2)∵AF=9,EF=12,EF⊥AC,
∴AE=![]()
∵OD∥AC,
∴△AEF∽△OED,
∴![]() ,
,
即![]()
∴OE=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
(2)如图,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.


端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
(3)如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC ,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:|a﹣2|+(b+1)2=0,求2ab2﹣a2b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形
 ,求出阴影部分的面积及其边长.
,求出阴影部分的面积及其边长.(3)把正方形
 放到数轴上,如图
放到数轴上,如图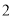 ,使得
,使得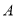 与
与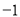 重合,点
重合,点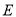 与
与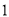 重合,点
重合,点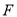 与点
与点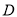 关于
关于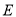 点对称,那么
点对称,那么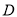 在数轴上表示的数为__________;点
在数轴上表示的数为__________;点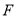 在数轴上表示的数为__________.
在数轴上表示的数为__________.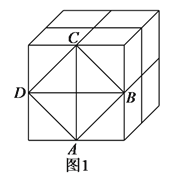
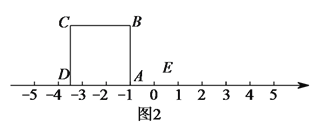
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简与求值:
(
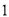 )已知当
)已知当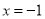 时,代数式
时,代数式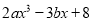 值为
值为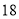 ,求代数式
,求代数式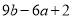 的值.
的值.(
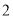 )已知
)已知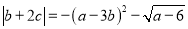 ,代数式
,代数式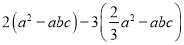 的值.
的值.(
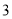 )若多项式
)若多项式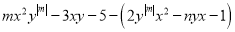 是关于
是关于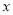 ,
, 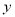 的四次二项式,求代数式
的四次二项式,求代数式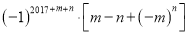 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=-x+4的图象与反比例
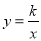 (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;
(2)连接OA,OB,求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州市从
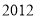 年
年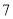 月
月 日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)
日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)档次
全年的用电量
电价(单位:元/度)
第一档
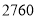 度以内(包括
度以内(包括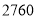 度)
度)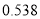
第二档
 至
至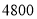 度(包含
度(包含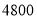 度)
度)
第三档
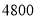 度以上
度以上
(
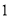 )小王家
)小王家 年全年的用电量是
年全年的用电量是 度,请计算小王家这年的电费付了多少元?
度,请计算小王家这年的电费付了多少元?(
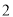 )小李家
)小李家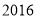 年
年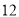 月份这个月的用电量是
月份这个月的用电量是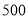 度,小李算出它们家的电费是
度,小李算出它们家的电费是 元,而供电局却收了小李家的电费
元,而供电局却收了小李家的电费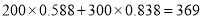 元,你知道其中的奥秘吗?请你来解释下.
元,你知道其中的奥秘吗?请你来解释下.(
 )小张家
)小张家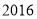 年全年用电量为
年全年用电量为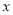 度,请用含
度,请用含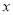 的代数式表示小张家全年应交的总电费,并把结果化简.
的代数式表示小张家全年应交的总电费,并把结果化简.
相关试题

