【题目】如图,在等腰Rt△ABC中,∠ACB=90![]() ,D为BC边上的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF.
,D为BC边上的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.

参考答案:
【答案】(1) 答案见解析;(2) 答案见解析
【解析】试题分析:
(1)由已知条件证:∠BDE=∠BFE=45°,从而可得:BF=BD,结合点D是CB的中点,可得BF=BD=CD;然后结合已知条件证:△ACD≌△CBF,从而可得:∠CAD=∠BCF,结合∠CAD+∠CDA=90![]() ,可得∠BCF+∠CDA=90
,可得∠BCF+∠CDA=90![]() ,这样就可得:∠AGC=90
,这样就可得:∠AGC=90![]() ,从而可得:AD⊥CF;
,从而可得:AD⊥CF;
(2)由(1)中BF=BD结合DE⊥AB可证:AB垂直平分DF,由此可得:AD=AF;由△ACD≌△CBF可得:AD=CF;两者结合可得:AF=CF,因此△ACF是等腰三角形.
试题解析:
(1)∵在等腰Rt△ABC中,∠ACB=90![]() ,
,
∴∠CBA=45![]() ,AC=BC .
,AC=BC .
又∵BF//AC, ∠ACB=90![]() ,
,
∴∠FBC=90![]() ,
,
∴∠FBE=45![]() .
.
又∵DE⊥AB,
∴∠BFE=45°,∠BDE=45°,
∴∠BFE=∠BDE,
∴BF=BD ,
∵D为BC的中点,
∴BD=CD,
∴ BF=CD.
在△ACD和△CBF中,  ,
,
∴ △ACD≌△CBF,
∴∠CAD=∠BCF,
又∵ ∠CAD+∠CDA=90![]() ,
,
∴∠BCF+∠CDA=90![]() ,
,
∴∠AGC=90![]() ,即AD⊥CF .
,即AD⊥CF .

(2)△ACF是等腰三角形,理由如下:
由(1)可知:△ACD≌△CBF;BD=BF,DE![]() AB,
AB,
∴CF=AD;DE=FE,
∴AB垂直平分DF,
∴AD=AF,
∴AF=CF ,
∴△ACF是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“综合与实践”学习活动准备制作一组三角形.记这些三角形的三边分别为
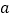 ,
, ,
, ,并且这些三角形三边的长度为大于
,并且这些三角形三边的长度为大于 且小于
且小于 的整数个单位长度,用记号(
的整数个单位长度,用记号(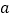 ,
, ,
, )(
)( )表示一个满足条件的三角形,如(
)表示一个满足条件的三角形,如( ,
, ,
, )表示边长分别为
)表示边长分别为 ,
, ,
, 个单位长度的一个三角形,请列举出所有满足条件的三角形.
个单位长度的一个三角形,请列举出所有满足条件的三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】4+12(x-y)+9(x-y)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在CCTV“开心辞典”栏目中,主持人问这样一道题目:“a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,请问:a,b,c三数之和是( )
A.-1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(a-3)(a-5)+1.
相关试题

