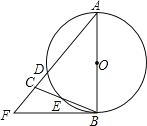
【题目】如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠A,tan∠CBF=
∠A,tan∠CBF=![]() ,则CF的长为( )
,则CF的长为( )
A.![]() B.
B.![]()
![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】A
【解析】
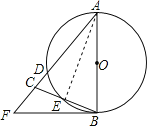
试题分析:连接AE,根据AB是直径,得出AE⊥BC,CE=EB,依据已知条件得出∠CBF=∠EAB,FB是圆的且线,进而得出CB的长,然后根据割线定理求得CD的长,最后根据切割线定理求得FC.
解:连接AE,
∵AB为直径,
∴AE⊥BC,
∵AB=AC,
∴∠EAB=![]() ∠CAB,EB=CE=
∠CAB,EB=CE=![]() CB,
CB,
∵∠CBF=![]() ∠CAB,tan∠CBF=
∠CAB,tan∠CBF=![]() ,
,
∴∠CBF=∠EAB,tan∠EAB=![]() =
=![]() ,
,
∴∠CBF+∠ABC=∠EAB+∠ABC=90°,
∴FB是⊙O的切线,
∴FB2=FDFA,
在RT△AEB中,AB=10,
∴EB=![]() ,
,
∴CB=2![]() ,CE=
,CE=![]() ,
,
∵CECB=CDAC,AC=10,
∴CD=2,
∴AD=AC﹣CD=8,
设CF=x,则FD=x+2,FA=10+x,FB2=AF2﹣AB2=(10+x)2﹣102,
∴(10+x)2﹣102=(x+2)(10+x),
整理得:x=![]() ,
,
∴CF=![]() ,
,
故应选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市实验中学学生步行到郊外旅行.高一(1)班学生组成前队,步行速度为4千米/时,高一(2)班学生组成后队,速度为6千米/时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时.
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)两队何时相距2千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加户外活动的情况,某校对初三学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)将条形统计图补画完整.
(2)求每天参加户外活动时间达到2小时的学生所占调查学生的百分比.
(3)这批参加调查的初三学生参加户外活动的平均时间是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC为菱形,点B、C在以点O为圆心的
 上,若OA=1cm,∠1=∠2,则
上,若OA=1cm,∠1=∠2,则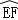 的长为 cm.
的长为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若︱x-1︱+︱y+2︱=0,求x+y的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(1)(x+1)2-x(2-x),其中x=2.
(2)-(-2a)3(-b3)2+(ab2)3,其中a=-1,b=2. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 要了解人们对“低碳生活”的了解程度,宜采用普查方式
B. 随机事件的概率为50%,必然事件的概率为100%
C. 一组数据3、4、5、5、6、7的众数和中位数都是5
D. 若甲组数据的方差是0.168,乙组数据的方差是0.034,则甲组数据比乙组数据稳定
相关试题

