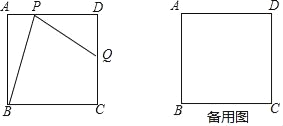
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() (0<x<2);(3)见解析
(0<x<2);(3)见解析
【解析】试题分析:(1)延长PQ交BC延长线于点E.设PD=x,由∠PBC=∠BPQ可得EB=EP,再根据AD//BC,QD=QC可得PD=CE,PQ=QE,从而得BE=EP= x+2, QP=![]() ,在Rt△PDQ中,根据勾股定理可得
,在Rt△PDQ中,根据勾股定理可得![]() ,从而求得
,从而求得![]() 的长,再根据正切的定义即可求得;
的长,再根据正切的定义即可求得;
(2)过点B作BH⊥PQ,垂足为点H,联结BQ,通过证明Rt△PAB Rt△PHB,得到AP = PH =x,通过证明Rt△BHQ Rt△BCQ,得到QH = QC= y,在Rt△PDQ中,根据 勾股定理可得PD2+QD2=PQ2,代入即可求得;
(3)存在,根据(2)中的两对全等三角形即可得.
试题解析:(1)延长PQ交BC延长线于点E,设PD=x,
∵∠PBC=∠BPQ,
∴EB=EP,
∵四边形ABCD是正方形,
∴AD//BC,∴PD∶CE= QD∶QC= PQ∶QE,
∵QD=QC,∴PD=CE,PQ=QE,
∴BE=EP= x+2,∴QP=![]() ,
,
在Rt△PDQ中,∵![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴![]() ,∴
,∴![]() ;
;
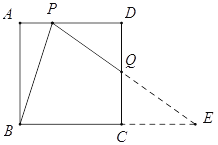
(2)过点B作BH⊥PQ,垂足为点H,联结BQ,
∵AD//BC,∴∠CBP=∠APB,∵∠PBC=∠BPQ,∴∠APB=∠HPB,
∵∠A=∠PHB=90°,∴BH = AB =2,∵PB = PB,∴Rt△PAB![]() Rt△PHB,
Rt△PHB,
∴AP = PH =x,
∵BC = BH=2,BQ = BQ,∠C=∠BHQ=90°,
∴Rt△BHQ![]() Rt△BCQ,∴QH = QC= y
Rt△BCQ,∴QH = QC= y
在Rt△PDQ中,∵![]() ,∴
,∴![]() ,
,
∴![]() ;
;

(3)存在,∠PBQ=45°.
由(2)可得, ![]() ,
, ![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若
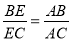 ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.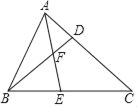
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与
与 轴交于点
轴交于点 (1,0)和点
(1,0)和点 ,与
,与 轴交于点
轴交于点 ,对称轴为直线
,对称轴为直线 =1.
=1.(1)求点
 的坐标(用含
的坐标(用含 的代数式表示)
的代数式表示)(2)连接
 、
、 ,若△
,若△ 的面积为6,求此抛物线的解析式;
的面积为6,求此抛物线的解析式;(3)在(2)的条件下,点
 为
为 轴正半轴上的一点,点
轴正半轴上的一点,点 与点
与点 ,点
,点 与点
与点 关于点
关于点 成中心对称,当△
成中心对称,当△ 为直角三角形时,求点
为直角三角形时,求点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)(x+3)(x﹣3)=3
(2)x2﹣2x﹣3=0(用配方法));
(3)(x-5)2=2(5-x)
(4)6x2﹣x﹣2=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阴影部分是边长是
 的大正方形剪去一个边长是
的大正方形剪去一个边长是 的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3幅图割拼方法中,其中能够验证平方差公式有___________(填序号)
的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3幅图割拼方法中,其中能够验证平方差公式有___________(填序号)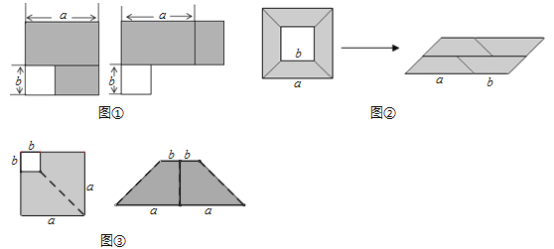
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 满足条件:(1)在
满足条件:(1)在 时,
时,  随
随 的增大而增大,在
的增大而增大,在 时,
时,  随
随 的增大而减小;(2)与
的增大而减小;(2)与 轴有两个交点,且两个交点间的距离小于
轴有两个交点,且两个交点间的距离小于 .以下四个结论:①
.以下四个结论:① ;②
;② ;③
;③ ;④
;④ ,说法正确的个数有( )个
,说法正确的个数有( )个A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
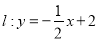 交
交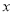 轴于
轴于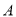 点,交
点,交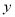 轴于
轴于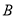 点,
点, 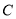 为
为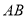 的中点,
的中点, 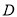 为射线
为射线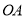 上一点,连
上一点,连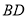 ,将
,将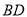 绕
绕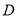 点顺时针旋转
点顺时针旋转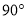 得线段
得线段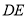 ,则
,则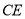 的最小值为__________.
的最小值为__________.
相关试题

