【题目】如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D。
(1)求证: ![]() ;
;
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即![]() ,如T(60°)=1.
,如T(60°)=1.
①理解巩固:T(90°)= ,T(120°)= ,若α是等腰三角形的顶角,则T(α)的取值范围是 ;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1)。
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
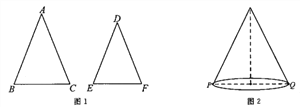
参考答案:
【答案】(1)证明见解析;(2)![]()
![]() 0<T(a)<2 11.6
0<T(a)<2 11.6
【解析】试题分析:(1)证明△ABC∽△DEF,根据相似三角形的性质解答即可;
(2)①根据等腰直角三角形的性质和等腰三角形的性质进行计算即可;
②根据圆锥的侧面展开图的知识和扇形的弧长公式计算,得到扇形的圆心角,根据T(A)的定义解答即可.
试题解析:(1)∵AB=AC,DE=DF,
∴![]() ,
,
又∵∠A=∠D,
∴△ABC∽△DEF,
∴![]() ;
;
(2)①如图1,∠A=90°,AB=AC,
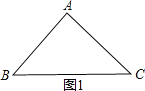
则![]() ,
,
∴T(90°)=![]() ,
,
如图2,∠A=120°,AB=AC,
作AD⊥BC于D,
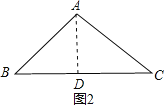
则∠B=30°,
∴BD=![]() AB,
AB,
∴BC=![]() AB,
AB,
∴T(120°)=![]()
∵AB-AC<BC<AB+AC,
∴0<T(α)<2,
②∵圆锥的底面直径PQ=8,
∴圆锥的底面周长为8π,即侧面展开图扇形的弧长为8π,
设扇形的圆心角为n°,
则![]() =8π,
=8π,
解得,n=160,
∵T(80°)≈1.29,
∴蚂蚁爬行的最短路径长为1.29×9≈11.6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
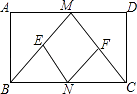
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=时,四边形MENF是正方形(只写结论,不需证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
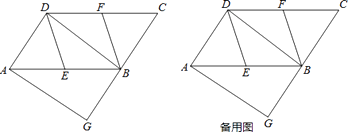
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形;
(3)请利用备用图分析,在(2)的条件下,若BE=4,∠DEB=120°,点M为BF的中点,当点P在BD边上运动时,求PF+PM的最小值,并求出此时线段BP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形三个内角度数的比是l:5:6,则其最大内角的度数为 ( )
A. 60°B. 75°C. 90°D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两条边长分别为10 cm和4 cm,那么它的周长为 _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过移项,将下列方程变形,错误的是( )
A. 由2x﹣3=﹣x﹣4,得2x﹣x=﹣4+3B. x+2=2x﹣7,得x-2x=﹣2-7
C. 5y﹣2=﹣6,得5y=﹣4D. 由x+3=2﹣4x,得5x=﹣1
相关试题

