【题目】株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.
参考答案:
【答案】解:设抛物线的解析式为: y=ax2,
∵A的坐标是(-10,10),
∴ 100a=10 ,
∴ a=0.1 ,
∴抛物线的解析式为: y=0.1x2 ,
又∵x=4 ,
∴ y=0.1×16=1.6,
∴点C坐标为(-4,-1.6),
又∵点D坐标为(-4,-10)
∴CD=10-1.6=8.4(米),
答:中柱左边第二根支柱CD的高度为8.4米.
【解析】设抛物线的解析式为: y=ax2,由已知得A的坐标是(-10,10),将此代入即可求出抛物线的解析式为: y=0.1x2 ,再根据已知条件求出
点C(-4,-1.6),又知点D(-4,-10),从而得CD=10-1.6=8.4(米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点A、M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
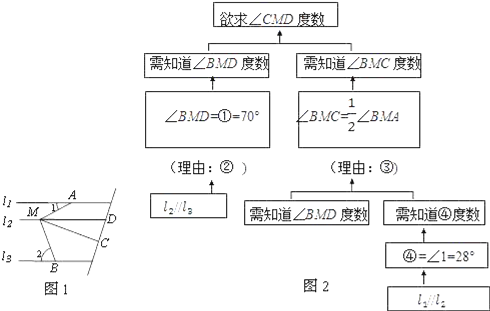
请问小坚的提示中①是∠ ,④是∠ .
理由②是: ;
理由③是: ;
∠CMD的度数是 °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D、E、F分别是BC、AD、BE上的中点,且△ABC的面积为8cm2,则△CEF的面积为( )

A.0.5cm2B.1cm2C.2cm2D.4cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在湖州创建国家卫生文明城市的过程中,张辉和夏明积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:①清理类岗位:清理花坛卫生死角;清理楼道杂物(分别用
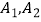 表示)。
表示)。
②宣传类岗位:垃圾分类知识宣传;交通安全知识宣传(分别用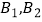 表示)。
表示)。
(1)张辉同学从四个岗位中随机选取一个报名,恰好选择清理类岗位概率为是;
(2)若张辉和夏明各随机从四个岗位中选一个报名,请你利用树状图或列表法求出他们恰好都选择同一个岗位的概率.
相关试题

