【题目】平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
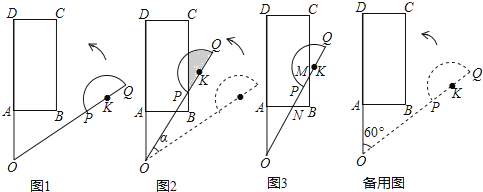
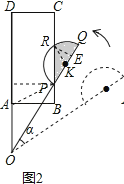
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
参考答案:
【答案】发现:α=30°,S阴影=![]() +
+![]() ;
;
拓展: BN=![]() ,0<x≤2
,0<x≤2![]() ﹣1;
﹣1;
探究: sinα的值为:![]() 或
或![]() 或
或![]() .
.
【解析】
试题分析:首先设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,则可求得∠RKQ的度数,于是求得答案;
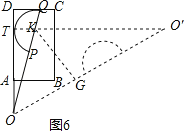
拓展:如图5,由∠OAN=∠MBN=90°,∠ANO=∠BNM,得到△AON∽△BMN,即可求得BN,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF,则可求出x的取值范围;
探究:半圆K与矩形ABCD的边相切,分三种情况:①半圆K与BC相切于点T,②当半圆K与AD相切于T,③当半圆K与CD切线时,点Q与点D重合,且为切点;分别求解即可求得答案.
解:发现:如图2,设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,
过点R作RE⊥KQ于点E,在Rt△OPH中,PH=AB=1,OP=2,
∴∠POH=30°,
∴α=60°﹣30°=30°,
∵AD∥BC,
∴∠RPO=∠POH=30°,
∴∠RKQ=2×30°=60°,
∴S扇形KRQ= =
=![]() ,
,
在Rt△RKE中,RE=RKsin60°=![]() ,
,
∴S△PRK=![]() RE=
RE=![]() ,
,
∴S阴影=![]() +
+![]() ;
;
拓展:如图5,
∵∠OAN=∠MBN=90°,∠ANO=∠BNM,
∴△AON∽△BMN,
∴![]() ,即
,即![]() ,
,
∴BN=![]() ,
,
如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF=![]() ﹣AO=2
﹣AO=2![]() ﹣1,
﹣1,
∴x的取值范围是0<x≤2![]() ﹣1;
﹣1;
探究:半圆K与矩形ABCD的边相切,分三种情况;
①如图5,半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,
则∠KSO=∠KTB=90°,
作KG⊥OO′于G,在Rt△OSK中,
OS=![]() =2,
=2,
在Rt△OSO′中,SO′=OStan60°=2![]() ,KO′=2
,KO′=2![]() ﹣
﹣![]() ,
,
在Rt△KGO′中,∠O′=30°,
∴KG=![]() KO′=
KO′=![]() ﹣
﹣![]() ,
,
∴在Rt△OGK中,sinα=![]() =
=![]() =
=![]() ,
,
②当半圆K与AD相切于T,如图6,同理可得sinα=![]() =
=![]() =
=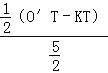 =
=![]() ;
;
③当半圆K与CD切线时,点Q与点D重合,且为切点,
∴α=60°,
∴sinα=sin60°=![]() ;
;
综上所述sinα的值为:![]() 或
或![]() 或
或![]() .
.

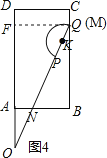
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.一组对边平行的四边形是梯形
B.有两个角是直角的四边形是直角梯形
C.只有相邻的两个角是直角的四边形是直角梯形
D.一组对边平行另一组对边相等的四边形是等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)17﹣8÷(﹣2)2+4×(﹣3) (2)2(2a2+9b)+3(﹣5a2﹣4b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年4月23日是“世界读书日”,为了了解某校八年级500名学生对“世界读书日”的知晓情况,从中随机抽取了50名学生进行调查.在这次调查中,样本是( )
A.500名学生 B.所抽取的50名学生对“世界读书日”的知晓情况
C.50名学生 D.每一名学生对“世界读书日”的知晓情况
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,AC=6,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不能作为直角三角形三边长的是( )
A. 8,15,17B. 5,12,13C. 2,3,4D. 7,24,25
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过平面内任意三点能画_____条直线.
相关试题

