【题目】如图,两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置,PA、PB与直线MN重合,且三角板PAC、三角板PBD均可绕点P逆时针旋转.
(1)直接写出∠DPC的度数.
(2)如图②,在图①基础上,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为5°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为1°/秒,(当PA转到与PM重合时,两三角板都停止转动),在旋转过程中,当PC与PB重合时,求旋转的时间是多少?
(3)在(2)的条件下,PC、PB、PD三条射线中,当其中一条射线平分另两条射线的夹角时,请直接写出旋转的时间.

参考答案:
【答案】(1)90°;(2)旋转的时间是30秒时PC与PB重合;(3)15秒或26.25秒或37.5秒时其中一条射线平分另两条射线的夹角.
【解析】
(1)易得∠DPC=180°-∠APC-∠BPD即可求
(2)只需设旋转的时间是t秒时PC与PB重合,列方程解可得
(3)一条射线平分另两条射线的夹角,分三种情况:当PD平分∠BPC时;当PC平分∠BPC时;当PB平分∠DPC时,计算每种情况对应的时间即可.
解:
(1)∠DPC=180°-∠APC-∠BPD=180°-60°-30°=90°
故答案为:90°
(2)设旋转的时间是t秒时PC与PB重合,根据题意列方程得
5t-t=30+90
解得t=30
又∵180÷5=36秒
∴30<36
故旋转的时间是30秒时PC与PB重合.
(3)设t秒时其中一条射线平分另两条射线的夹角,分三种情况:
①当PD平分∠BPC时,5t-t=90-30,解得t=15
②当PC平分∠BPC时,![]() ,解得t=26.25
,解得t=26.25
③当PB平分∠DPC时,5t-t=90-2×30,解得t=37.5
故15秒或26.25秒或37.5秒时其中一条射线平分另两条射线的夹角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB//DG, AD∥EF,
(1)试说明:
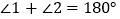 ;
;(2) 若DG是∠ADC的平分线,
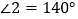 ,求∠B的度数.
,求∠B的度数.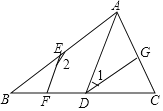
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:
价格/类型
A型
B型
进价(元/只)
15
35
标价(元/只)
25
50
(1)这两种文具盒各购进多少只?
(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
(1)求A、B两点的坐标;
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.

(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG= ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
相关试题

