Question

【题目】如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线相交于点E，且∠A=∠EBC．

（1）求证：BE是⊙O的切线；
（2）已知CG∥EB，且CG与BD、BA分别相交于点F、G，若BGBA=48，FG= ，DF=2BF，求AH的值．

Answer 1

【答案】
（1）证明：连接CD，

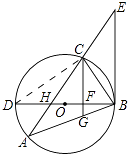
∵BD是直径，

∴∠BCD=90°，即∠D+∠CBD=90°，

∵∠A=∠D，∠A=∠EBC，

∴∠CBD+∠EBC=90°，

∴BE⊥BD，

∴BE是⊙O切线．

（2）解：∵CG∥EB，

∴∠BCG=∠EBC，

∴∠A=∠BCG，

∵∠CBG=∠ABC

∴△ABC∽△CBG，

∴ = ，即BC2=BGBA=48，

∴BC=4 ，

∵CG∥EB，

∴CF⊥BD，

∴△BFC∽△BCD，

∴BC2=BFBD，

∵DF=2BF，

∴BF=4，

在Rt△BCF中，CF= =4 ，

∴CG=CF+FG=5 ，

在Rt△BFG中，BG= =3 ，

∵BGBA=48，

∴ 即AG=5 ，

∴CG=AG，

∴∠A=∠ACG=∠BCG，∠CFH=∠CFB=90°，

∴∠CHF=∠CBF，

∴CH=CB=4 ，

∵△ABC∽△CBG，

∴ = ，

∴AC= = ，

∴AH=AC﹣CH= ．

【解析】（1）连接CD，利用直径上的圆周角为直角可得∠D+∠CBD=90°，再利用圆周角定理可得∠CBD+∠EBC=90°，进而得证；
（2）先证△ABC∽△CBG，可得BC2=BGBA，从而求得BC的长，再由△BFC∽△BCD可得BF的长，进而求得CH、BG、CG的长，再用△ABC∽△CBG利用对应边长比例求得AC的长，又AH=AC-CH可求得结果.
【考点精析】通过灵活运用三角形的外接圆与外心和切线的判定定理，掌握过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心；切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题．