【题目】为了防止水土流失,某村开展绿化荒山活动,计划经过若干年使本村绿化总面积新增360万平方米.自2014年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.问实际每年绿化面积多少万平方米?
参考答案:
【答案】实际每年绿化面积为54万平方米.
【解析】分析:设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米,根据工作时间=工作总量÷工作效率结合提前4年完成任务.即可得出关于x的分式方程,解之经检验后即可得出结论.
详解:设原计划每年绿化面积为x万平方米,根据题意,得:
![]()
解得:x=33.75,
经检验x=33.75是原分式方程的解,
则1.6x=1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市水果批发部门欲将 A 市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为 200 元/ 时.其它主要参考数据如下:
运输工具
途中平均速度(千米/ 时)
运费(元/ 千米)
装卸费用(元)
火车
100
15
2000
汽车
80
20
900
运输过程中,火车因多次临时停车,全程在路上耽误 2 小时 45 分钟,火车的总支出费用与汽车的总支出费用相同,请问某市与本地的路程是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)对于任意正实数a、b,
∵(
 ﹣
﹣ )2≥0,
)2≥0,∴a﹣2
 +b≥0,
+b≥0,∴a+b≥2
 ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2 ).
).(1)(获得结论)在a+b≥2
 (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,则a+b≥2
 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 .
.根据上述内容,回答下列问题:若m>0,只有当m= 时,m+
 有最小值 .
有最小值 .(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=
 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y= (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.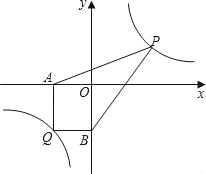
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代有着辉煌的数学成就,《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,求他选中《九章算术》的概率;
(2)小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容,用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.

被调查的捐款人数分组统计表:
组别
捐款额x/元
人数
A
1≤x<10
a
B
10≤x<20
100
C
20≤x<30
______
D
30≤x<40
______
E
40≤x
______
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.
(1)求证:四边形FBGH是菱形;
(2)求证:四边形ABCH是正方形.
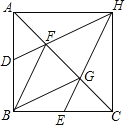
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是正方形
是正方形 的边
的边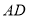 上的动点,
上的动点,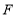 是边
是边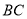 延长线上的一点,且
延长线上的一点,且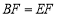 ,
,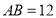 ,设
,设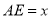 ,
,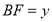 .
.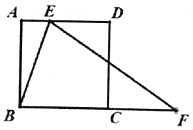
(1)当
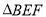 是等边三角形时,求
是等边三角形时,求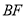 的长;
的长;(2)求
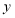 与
与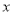 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;(3)把
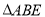 沿着直线
沿着直线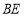 翻折,点
翻折,点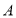 落在点
落在点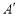 处,试探索:
处,试探索: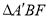 能否为等腰三角形?如果能,请求出
能否为等腰三角形?如果能,请求出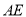 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.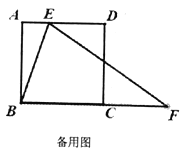
相关试题

