【题目】如图1,在四边形ABCD中,AD∥BC,∠B=∠C=60°,P、Q同时从B出发,以每秒1单位长度分别沿B﹣A﹣D﹣C和B﹣C﹣D方向运动至相遇时停止,设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2所示,则下列结论错误的个数( )
①当t=4秒时,S=4 ![]() ②AD=4③当4≤t≤8时,S=2
②AD=4③当4≤t≤8时,S=2 ![]() t④当t=9秒时,BP平分四边形ABCD的面积.
t④当t=9秒时,BP平分四边形ABCD的面积.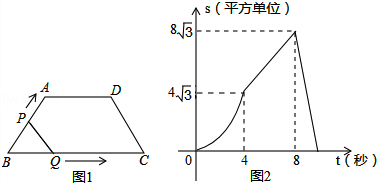
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:由答图2所示,动点运动过程分为三个阶段:(1)OE段,函数图象为抛物线,运动图形如答图1﹣1所示.
此时点P在线段AB上、点Q在线段BC上运动.
△BPQ为等边三角形,其边长BP=BQ=t,高h= ![]() t,
t,
∴S= ![]() BQh=
BQh= ![]() t
t ![]() t=
t= ![]() t2 .
t2 .
由函数图象可知,当t=4秒时,S=4 ![]() ,故选项A正确.(2)EF段,函数图象为直线,运动图形如答图1﹣2所示.
,故选项A正确.(2)EF段,函数图象为直线,运动图形如答图1﹣2所示.
此时点P在线段AD上、点Q在线段BC上运动.
由函数图象可知,此阶段运动时间为4s,
∴AD=1×4=4,故选项B正确.
设直线EF的解析式为:S=kt+b,将E(4,4 ![]() )、F(8,8
)、F(8,8 ![]() )代入得:
)代入得:![]() ,
,
解得 ![]() ,
,
∴S= ![]() t,故选项C错误.(3)FG段,函数图象为直线,运动图形如答图1﹣3所示.
t,故选项C错误.(3)FG段,函数图象为直线,运动图形如答图1﹣3所示.
此时点P、Q均在线段CD上运动.
设梯形高为h,则S梯形ABCD= ![]() (AD+BC)h=
(AD+BC)h= ![]() (4+8)h=6h;
(4+8)h=6h;
当t=9s时,DP=1,则CP=3,
∴S△BCP= ![]() S△BCD=
S△BCD= ![]() ×
× ![]() ×8×h=3h,
×8×h=3h,
∴S△BCP= ![]() S梯形ABCD , 即BP平分梯形ABCD的面积,故选项D正确.
S梯形ABCD , 即BP平分梯形ABCD的面积,故选项D正确.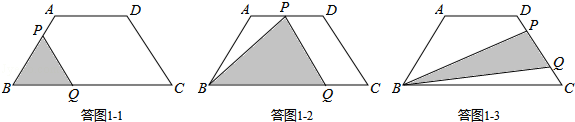
综上所述,错误的结论是C.
故选:C.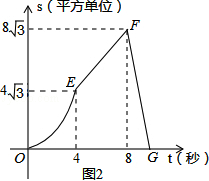
【考点精析】认真审题,首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣3x+12中x_________ 时,y<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD·OE;
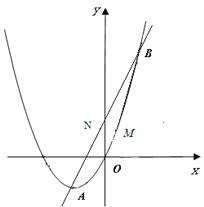
(3)若cos∠BAD=
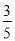 ,BE=6,求OE的长.
,BE=6,求OE的长.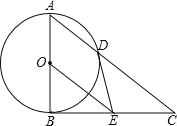
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)求表示户外活动时间1小时的扇形圆心角的度数;
(4)本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节前夕,某校为学生购买了A、B两种品牌的粽子共400个,已知B品牌粽子的单价比A品牌粽子的单价的2倍少6元.
(1)当买A品牌100个,B品牌粽子300个时,学校所花费用为4500元.求A、B两种品牌粽子各自的单价;
(2)在两种品牌粽子单价不变的情况下,由于资金临时出现状况,所花费用不超过4000元,问至少买A品牌粽子多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB , AD交于点A . C为直线AD上一点(不与点A , D重合).过点C在BC的右侧作射线CE⊥BC , 过点D作直线DF∥AB , 交CE于点G(G与D不重合).

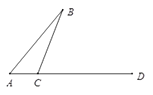
(1)如图1,若点C在线段AD上,且∠BCA为钝角.①按要求补全图形;②判断∠B与∠CGD的数量关系,并证明.
(2)若点C在线段DA的延长线上,请直接写出∠B与∠CGD的数量关系;
(3)请你结合本题的题意提出一个新的拓展问题 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+2x+
 与x轴有两个交点,且k为正整数.
与x轴有两个交点,且k为正整数.(1)求k的值;
(2)当二次函数y=x2+2x+
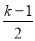 图象经过原点时,直线y=3x+2与之交于A、B两点,若M是抛物线上在直线y=3x+2下方的一个动点,△MAB面积是否存在最大值?若存在,请求出M点坐标,并求出△MAB面积最大值;若不存在,请说明理由.
图象经过原点时,直线y=3x+2与之交于A、B两点,若M是抛物线上在直线y=3x+2下方的一个动点,△MAB面积是否存在最大值?若存在,请求出M点坐标,并求出△MAB面积最大值;若不存在,请说明理由.(3)将(2)中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分保持不变,翻折后的图象与原图象x轴上方的部分组成一个新图象.若直线y=kx+2(k>0)与该新图象恰好有三个公共点,求k的值.
相关试题

