搜索
【题目】重庆出租车计费的方法如图所示，x(km)表示行驶里程，y(元)表示车费，请根据图象解答下列问题：
(1)该地出租车起步价是_____元；
(2)当x＞2时，求y与x之间的关系式；
(3)若某乘客一次乘出租车的里程为18km，则这位乘客需付出租车车费多少元？
参考答案：
【答案】(1)10；(2)y＝2x+6；(3)这位乘客需付出租车车费42元．
【解析】
(1)由图象知x＝﹣0时，y＝10可得答案；
(2)先求得出租车每公里的单价，根据车费＝起步价+超出部分费用可得函数解析式；
(3)将x＝18代入(2)中所求函数解析式．
解：(1)由函数图象知，出租车的起步价为10元，
故答案为：10；
(2)当x＞2时，每公里的单价为(14﹣10)÷(4﹣2)＝2，
∴当x＞2时，y＝10+2(x﹣2)＝2x+6；
(3)当x＝18时，y＝2×18+6＝42元，
答：这位乘客需付出租车车费42元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题情景：如图1，在等腰直角三角形ABC中∠ACB＝90°，BC＝a．将AB绕点B顺时针旋转90°得到线段BD，连接CD，过点D作△BCD的BC边上的高DE．
易证△ABC≌△BDE，从而得到△BCD的面积为
．简单应用：如图2，在Rt△ABC中，∠ACB＝90°，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，用含a的代数式表示△BCD的面积，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB⊥AC，CD、BE分别是△ABC的角平分线，AG∥BC，AG⊥BG，下列结论：①∠BAG＝2∠ABF；②BA平分∠CBG；③∠ABG＝∠ACB；④∠CFB＝135°，其中正确的结论有（ ）个
A.1B.2C.3D.4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一次函数y＝2x的图象与反比例函数y＝
（x＞0），y＝
（x＞0）的图象分别交于P，Q两点，点P为OQ的中点，Rt△ABC的直角顶点A是双曲线y＝（x＞0）上一动点，顶点B，C在双曲线y＝（x＞0）上，且两直角边均与坐标轴平行．（1）直接写出k的值；
（2）△ABC的面积是否变化？若不变，求出△ABC的面积；若变化，请说明理由；
（3）直线y＝2x是否存在点D，使得以A，B，C，D为顶点的四边形是平行四边形，若存在，求出点A的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
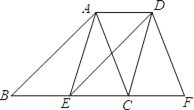
查看答案和解析>>【题目】如图，已知点E，C在线段BF上，BE＝EC＝CF，AB∥DE，∠ACB＝∠F．
(1)求证：△ABC≌△DEF；
(2)求证：四边形ACFD为平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】矗立在莲花山的邓小平雕像气宇轩昂，这是中国第一座以城市雕塑形式竖立的邓小平雕像。铜像由像体AD和底座CD两部分组成。某校数学课外小组在地面的点B处测得点A的仰角∠ABC=67°，点D的仰角∠DBC=30°，已知CD=2米，求像体AD的高度。（最后结果精确到1米，参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.4，
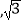≈1.7）
-
科目： 来源： 题型：
查看答案和解析>>【题目】学生小明、小华为了解本校八年级学生每周上网的时间，各自进行了抽样调查．小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间，算得这些学生平均每周上网时间为2.5h；小华从全体320名八年级学生名单中随机抽取了40名学生，调查了他们每周上网的时间，算得这些学生平均每周上网时间为1.2h．小明与小华整理各自样本数据，如表所示．
时间段（h/周）
小明抽样人数
小华抽样人数
0～1
6
22
1～2
10
10
2～3
16
6
3～4
8
2
（每组可含最低值，不含最高值）
请根据上述信息，回答下列问题：
（1）你认为哪位学生抽取的样本具有代表性？_____．
估计该校全体八年级学生平均每周上网时间为_____h；
（2）在具有代表性的样本中，中位数所在的时间段是_____h/周；
（3）专家建议每周上网2h以上（含2h）的同学应适当减少上网的时间，根据具有代表性的样本估计，该校全体八年级学生中有多少名学生应适当减少上网的时间？
相关试题
