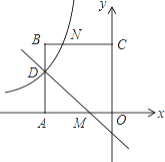
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OMP的面积等于2,求点P的坐标.
参考答案:
【答案】(1)y=-![]() ,y=-x-1(2)(-5,4)(3,-4)
,y=-x-1(2)(-5,4)(3,-4)
【解析】分析:(1)由正方形OABC的顶点C坐标,确定出边长,及四个角为直角,根据AD=2DB,求出AD的长,确定出D坐标,代入反比例解析式求出m的值,再由AM=2MO,确定出MO的长,即M坐标,将M与D坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)把y=3代入反比例解析式求出x的值,确定出N坐标,得到NC的长,设P(x,y),根据△OPM的面积等于2,求出y的值,进而得到x的值,确定出P坐标即可.
详解:(1)∵正方形OABC的顶点C(0,3),
∴OA=AB=BC=OC=3,![]()
∵AD=2DB,
∴AD=23AB=2,
∴D(3,2),
把D坐标代入![]() 得:m=6,
得:m=6,
∴反比例解析式为![]()
∵AM=2MO,
∴![]() 即M(1,0),
即M(1,0),
把M与D坐标代入y=kx+b中得:![]()
解得:k=b=1,
则直线DM解析式为y=x1;
(2)设P(x,y),
∵△OPM的面积等于2,
∴![]() 即|y|=4,
即|y|=4,
解得:y=4
当y=4时,x=5,当y=4,x=3,
则P坐标为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,文具店老板购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号
进价(元/只)
售价(元/只)
A型
10
14
B型
15
22
(1)老板如何进货,能使进货款恰好为1350元?
(2)要使销售文具所获利润不少于500元,那么老板最多能购进A型文具多少只?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,四边形ABCD是平行四边形,E,F是对角线AC上的两点,AE=CF.
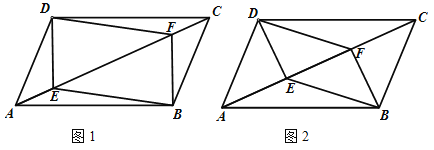
(1)求证:四边形DEBF是平行四边形;
(2)如果AE=EF=FC,请直接写出图中2所有面积等于四边形DEBF的面积的三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店欲购进A、B两种商品,若购进A种商品5件,B种商品3件,共需450元;若购进A种商品10件,B种商品8件,共需1000元.
(1)购进A、B两种商品每件各需多少元?
(2)该商店购进足够多的A、B两种商品,在销售中发现,A种商品售价为每件80元,每天可销售100件,现在决定对A种商品在每件80元的基础上降价销售,每件每降价1元,多售出20件,该商店对A种商品降价销售后每天销量超过200件;B种商品销售状况良好,每天可获利7000元,为使销售A、B两种商品每天总获利为10000元,A种商品每件降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮将笔记本电脑水平放置在桌子上,显示屏OA与底板OB所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架BCO'后,电脑转到B O′A′位置(如图3),侧面示意图为图4.已知OA=OB=28cm,O′C⊥OB于点C,O′C=14cm.
(参考数据:
 ,
,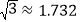 ,
,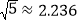 )
)(1)求∠CBO'的度数.
(2)显示屏的顶部A'比原来升高了多少cm?(结果精确到0.1cm)
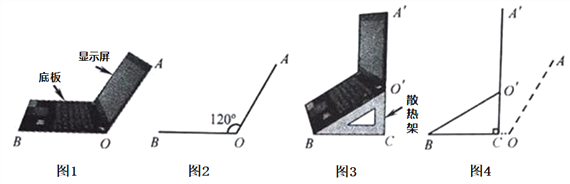
(3)如图4,垫入散热架后,要使显示屏O′A′与水平线的夹角仍保持120°,则显示屏O′A′应绕点O'按顺时针方向旋转多少度?(不写过程,只写结果)
-
科目: 来源: 题型:
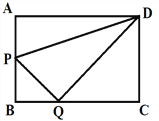
查看答案和解析>>【题目】在矩形ABCD中,AB=3,AD=4,动点P从点B出发,以每秒1个单位的速度,沿BA向点A移动;同时点Q从点C出发,以每秒2个单位的速度,沿CB向点B移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤2),解答下列问题:
(1)当x为何值时,PQ⊥DQ;
(2)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最小值?并求出最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的
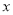 值为5,可发现第一次输出的结果为8,第二次输出的结果为4,…,请你探索第2020次输出的结果为( )
值为5,可发现第一次输出的结果为8,第二次输出的结果为4,…,请你探索第2020次输出的结果为( )
A.2B.1C.6D.4
相关试题

