【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
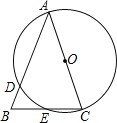
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
参考答案:
【答案】(1)见解析;(2)9.
【解析】
试题分析:(1)连结AE,如图,根据圆周角定理,由AC为⊙O的直径得到∠AEC=90°,然后利用等腰三角形的性质即可得到BE=CE;
(2)连结DE,如图,证明△BED∽△BAC,然后利用相似比可计算出AB的长,从而得到AC的长.
(1)证明:连结AE,如图,
∵AC为⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
而AB=AC,
∴BE=CE;
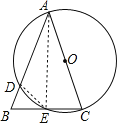
(2)连结DE,如图,
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,
而∠DBE=∠CBA,
∴△BED∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BA=9,
∴AC=BA=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1) 5( m2 )6 -3 (-m4)3 (2) 214×(-
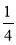 )7
)7(3)
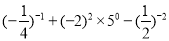 (4) (x-y)
(4) (x-y) (y-x)
(y-x) — 2[(x-y)3 ]3
— 2[(x-y)3 ]3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )

A.2海里 B.2sin55°海里 C.2cos55°海里 D.2tan55°海里
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.
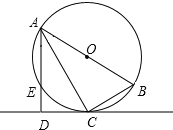
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2
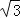 cm,求弦AE的长.
cm,求弦AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一边长是6cm,另一边长是3cm,则周长为______________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅准备用长为8cm的铜丝剪成两段,以围成两个正方形的线圈,设剪成的两段铜丝中的一段的长为xcm,围成的两个正方形的面积之和为Scm2.
(1)求S与x的函数关系式,并写出自变量的取值范围;
(2)当x取何值时,S取得最小值,并求出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(2a+b)2-(3a-b)2+5a(a-b),其中a =1,b=—1.
相关试题

