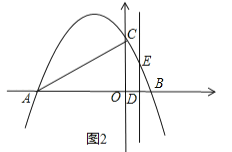
【题目】如图,抛物线![]() 与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.
与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)设四边形DECO的面积为s,求s关于t的函数表达式.

参考答案:
【答案】(1)![]() ,对称轴为:直线x=﹣
,对称轴为:直线x=﹣![]() ;(2)t=
;(2)t=![]() 或
或![]() ;(3)
;(3)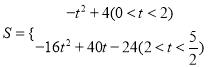 .
.
【解析】试题分析:(1)把A(﹣4,0),B(1,0),点C(0,2)即可得到结论;
(2)由题意得AD=2t,DF=AD=2t,OF=4﹣4t,由于直线AC的解析式为: ![]() ,得到E(2t﹣4,t),①当∠EFC=90°,则△DEF∽△OFC,根据相似三角形的性质得到结论;②当∠FEC=90°,根据等腰直角三角形的性质得到结论;③当∠ACF=90°,根据勾股定理得到结论;
,得到E(2t﹣4,t),①当∠EFC=90°,则△DEF∽△OFC,根据相似三角形的性质得到结论;②当∠FEC=90°,根据等腰直角三角形的性质得到结论;③当∠ACF=90°,根据勾股定理得到结论;
(3)求得直线BC的解析式为:y=﹣2x+2,当D在y轴的左侧时,当D在y轴的右侧时,如图2,根据梯形的面积公式即可得到结论.
试题解析:解:(1)把A(﹣4,0),B(1,0),点C(0,2)代入![]() 得:
得: 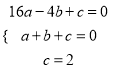 ,解得:
,解得:  ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() ,对称轴为:直线x=﹣
,对称轴为:直线x=﹣![]() ;
;
(2)存在,∵AD=2t,∴DF=AD=2t,∴OF=4﹣4t,∴D(2t﹣4,0),∵直线AC的解析式为: ![]() ,∴E(2t﹣4,t),∵△EFC为直角三角形,分三种情况讨论:
,∴E(2t﹣4,t),∵△EFC为直角三角形,分三种情况讨论:
①当∠EFC=90°,则△DEF∽△OFC,∴ ![]() ,即
,即![]() ,解得:t=
,解得:t=![]() ;
;
②当∠FEC=90°,∴∠AEF=90°,∴△AEF是等腰直角三角形,∴DE=![]() AF,即t=2t,∴t=0,(舍去),③当∠ACF=90°,则AC2+CF2=AF2,即(42+22)+[22+(4t﹣4)2]=(4t)2,解得:t=
AF,即t=2t,∴t=0,(舍去),③当∠ACF=90°,则AC2+CF2=AF2,即(42+22)+[22+(4t﹣4)2]=(4t)2,解得:t=![]() ,∴存在某一时刻t,使得△EFC为直角三角形,此时,t=
,∴存在某一时刻t,使得△EFC为直角三角形,此时,t=![]() 或
或![]() ;
;
(3)∵B(1,0),C(0,2),∴直线BC的解析式为:y=﹣2x+2,当D在y轴的左侧时,S=![]() (DE+OC)OD=
(DE+OC)OD=![]() (t+2)(4﹣2t)=﹣t2+4 (0<t<2);
(t+2)(4﹣2t)=﹣t2+4 (0<t<2);
当D在y轴的右侧时,如图2,∵OD=4t﹣4,DE=﹣8t+10,S=![]() (DE+OC)OD=
(DE+OC)OD=![]() (﹣8t+10+2)(4t﹣4),即
(﹣8t+10+2)(4t﹣4),即![]() (2<t<
(2<t<![]() ).
).
综上所述: 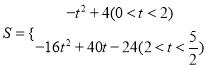
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点A的坐标为(5,0),点B的坐标为(3,2),直线
中,点A的坐标为(5,0),点B的坐标为(3,2),直线 经过原点和点B,直线
经过原点和点B,直线 经过点A和点B.
经过点A和点B.(1)求直线
 ,
,  的函数关系式;
的函数关系式;(2)根据函数图像回答:不等式
 的解集为 ;
的解集为 ;(3)若点
 是
是 轴上的一动点,经过点P作直线
轴上的一动点,经过点P作直线 ∥
∥ 轴,交直线
轴,交直线 于点C,交直线
于点C,交直线 于点D,分别经过点C,D向
于点D,分别经过点C,D向 轴作垂线,垂足分别为点E, F,得长方形CDFE.
轴作垂线,垂足分别为点E, F,得长方形CDFE.①若设点P的横坐标为m,则点C的坐标为(m, ),点D的坐标为(m, );(用含字母m的式子表示)
②若长方形CDFE的周长为26,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是______(用含m的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】规定“*”是一种运算符号,且a*b=ab﹣3a,则计算(﹣3)*2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下面的解答过程补充完整:
如图,已知EF⊥AB,CD⊥AB,AC⊥BC,
 ,求证:DG⊥BC
,求证:DG⊥BC 
证明:∵ EF⊥AB,CD⊥AB(已知)
∴
 (___________)
(___________)∴EF∥CD (_____________________________)
∴
 ____(_________________________)
____(_________________________)∵
 (已知)
(已知) ∴
 _____(______________________)
_____(______________________)∴DG∥AC(______________________________)
∴
 (_____________________________)
(_____________________________) ∵AC⊥BC(已知)
∴

∴
 ,即DG⊥BC
,即DG⊥BC -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组式子中,两个单项式是同类项的是()
A. 2a与a2 B. 5xy2与y2x C. ab与a2b D. 0.3x2y与0.3a2b
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. b3b3=2b3 B. (a+b)2=a2+b2
C. (a5)2=a10 D. a–(b+c)=a–b+c
相关试题

