【题目】如图,在Rt△ABC中,∠C![]() 90°,AC
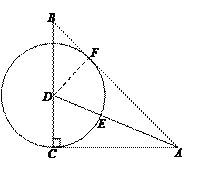
90°,AC![]() BC,AD是△ABC的角平分线,以D为圆心,DC为半径作⊙D,交AD于点E.
BC,AD是△ABC的角平分线,以D为圆心,DC为半径作⊙D,交AD于点E.
(1)判断直线AB与⊙D的位置关系并证明.
(2)若AC![]() 1,求
1,求![]() 的长.
的长.

参考答案:
【答案】(1)见解析;(2)![]()
【解析】分析:(1)根据“作垂直,证相等”可证明AB与⊙D相切;
(2)分别求出![]() 所在圆的半径和圆心有的度数,代入弧长公式进行计算即可得解.
所在圆的半径和圆心有的度数,代入弧长公式进行计算即可得解.
详解:(1)AB与⊙D相切.
证明:过点D作DF⊥AB,垂足为F.
∵AD是Rt△ABC的角平分线,∠C![]() 90°,
90°,
∴DF![]() DC,
DC,
即d![]() r,
r,
∴AB与⊙D相切.
(2)∵∠C![]() 90°,AC
90°,AC![]() BC
BC![]() 1,∴∠BAC
1,∴∠BAC![]() ∠B
∠B![]() 45°,AB
45°,AB![]() .
.
∵DF⊥AB,∴∠BDF![]() ∠B
∠B![]() 45°,∴BF
45°,∴BF![]() DF.
DF.
∵AB、AC分别与⊙D相切,∴AF![]() AC
AC![]() 1.
1.
设⊙D的半径为r.易得BF![]() ,BD
,BD![]() ,
,
∴![]() ,∴r
,∴r![]() .
.
∵AD是Rt△ABC的角平分线,∠BAC![]() 45°,
45°,
∴∠DAC![]()
![]() ∠BAC
∠BAC![]() 22.5°.
22.5°.
又∵∠C![]() 90°,∴∠CDE
90°,∴∠CDE![]() 67.5°.
67.5°.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形
 中,
中, 点在
点在 上,并且
上,并且 ,分别以
,分别以 、
、 为折痕进行折叠并压平,如图②,若图②中
为折痕进行折叠并压平,如图②,若图②中 ,则
,则 的度数为______度.
的度数为______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测、距某城市
 的正南方向
的正南方向 千米
千米 处有一台风中心,其中心最大风力为
处有一台风中心,其中心最大风力为 级,每远离台风中心
级,每远离台风中心 千米风力就会减弱一级,该台风中心现正以
千米风力就会减弱一级,该台风中心现正以 千米/时的速度沿北偏东
千米/时的速度沿北偏东 方向往
方向往 移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响
移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响 该城市是否会受到这交台风的影响?请说明理由;
该城市是否会受到这交台风的影响?请说明理由; 若会受到台风影响,那么台风影响该城市持续时间有多少?
若会受到台风影响,那么台风影响该城市持续时间有多少? 该城市受到台风影响的最大风力为几级?
该城市受到台风影响的最大风力为几级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为 ( )

A. 2
 B. (
B. ( +1) C. (
+1) C. ( +2) D. (
+2) D. ( +1)
+1) -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别
步数分组
频数
A
5500≤x<6500
2
B
6500≤x<7500
10
C
7500≤x<8500
m
D
8500≤x<9500
3
E
9500≤x<10500
n

请根据以上信息解答下列问题:
(1)填空:m= ______ ,n= ______ ;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是边BC上的中线,AE∥BC,DE∥AB,DE与AC交于点O,连接CE.
(1)求证:AD=EC;
(2)若∠BAC=90°,求证:四边形ADCE是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD,BE平分
 ,交AD于点E,F是BE的中点,G是BC的中点,连按EC,若
,交AD于点E,F是BE的中点,G是BC的中点,连按EC,若 ,
, ,则FG的长为________。
,则FG的长为________。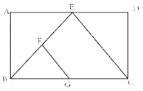
相关试题

