【题目】已知∠AOB=90°,OC是∠AOB的平分线,按以下要求解答问题.
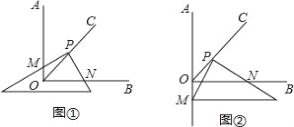
(1)将三角板的直角顶点P在射线OC上移动,两直角边分别与OA,OB交于M,N,如图①,求证:PM=PN;
(2)将三角板的直角顶点P在射线OC上移动,一条直角边与OB交于N,另一条直角边与射线OA的反向延长线交于点M,并猜想此时①中的结论PM=PN是否成立,并说明理由 .
参考答案:
【答案】(1)见解析(2)成立
【解析】
(1)过P作PE⊥OA,PF⊥OB,由OC为∠AOB的平分线,利用角平分线定理得到PE=PF,利用同角的余角相等得到一对角相等,利用ASA得到△PME与△PNF全等,利用全等三角形的对应边相等即可得证;
(2)过P作PE⊥OA,PF⊥OB,由OC为∠AOB的平分线,利用角平分线定理得到PE=PF,利用同角的余角相等得到一对角相等,利用ASA得到△PME与△PNF全等,利用全等三角形的对应边相等即可得证.
(1)过P作PE⊥OA于E,PF⊥OB于F,
∵OC是∠AOB的平分线,
∴![]()
∵![]()
∴∠MPE=∠NPF,
在△PME和△PNF中,
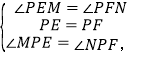
∴△PME≌△PNF(ASA),
∴PM=PN.
(2)过P作PE⊥OA于E,PF⊥OB于F,
∵OC是∠AOB的平分线,
∴![]()
∵![]()
∴∠MPE=∠NPF,
在△PME和△PNF中,
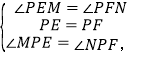
∴△PME≌△PNF(ASA),
∴PM=PN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

-
科目: 来源: 题型:
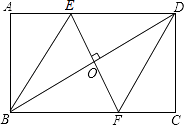
查看答案和解析>>【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE=AE,则边BC的长为( )
A.2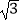
B.3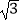
C.
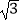
D.6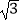
-
科目: 来源: 题型:
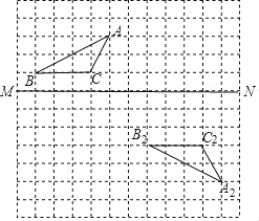
查看答案和解析>>【题目】在图示的方格纸中,(1)画出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
(3)在直线MN上找一点P,使得PB+PA最短.(不必说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)(问题引领)
问题1:在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明
△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是________________.

(探究思考)
问题2:若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF=
 ∠BCD, 问题1的结论是否仍然成立?请说明理由.
∠BCD, 问题1的结论是否仍然成立?请说明理由.
(拓展延伸)
问题3:在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是
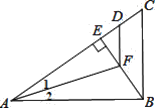
A. BF=DF B. ∠1=∠EFD C. BF>EF D. FD∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD,BC相交于点O,OA=OD,OB=OC.下列结论正确的是( )

A. △AOB≌△DOC B. △ABO≌△DOC C. ∠A=∠C D. ∠B=∠D
相关试题

