【题目】小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题:
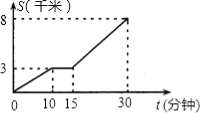
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
参考答案:
【答案】(1)3千米;修车用了15﹣10=5(分钟);(2)30分钟;(3)他比实际情况早到学校3.3分钟.
【解析】
试题看一个函数图像,需要看清楚x轴和y轴表示什么,水平线表示y没变化,上升直线表示y匀速增加,直线的斜率就是增加的速度,(1)由题,在10分钟时,S没变化,说明在此处爆胎,小亮行了3千米时,自行车“爆胎”;不变的时间一直到15分钟,故修车用了15﹣10=5(分钟);(2)从图像上直接可以看到小亮到校路上共用了30分钟;(3)小亮修车前的速度为3÷10=![]() (千米/分钟),按此速度到校共需时间为8÷
(千米/分钟),按此速度到校共需时间为8÷![]() =
=![]() (分钟),30-
(分钟),30-![]() =
=![]() ≈3.3(分钟),则他比实际情况早到学校3.3分钟.
≈3.3(分钟),则他比实际情况早到学校3.3分钟.
试题解析:(1)由题,在10分钟时,S没变化,说明在此处爆胎,小亮行了3千米时,自行车“爆胎”;
不变的时间一直到15分钟,故修车用了15﹣10=5(分钟);
(2)从图像上直接可以看到小亮到校路上共用了30分钟;
(3)小亮修车前的速度为3÷10=![]() (千米/分钟),
(千米/分钟),
按此速度到校共需时间为8÷![]() =
=![]() (分钟),
(分钟),
30-![]() =
=![]() ≈3.3(分钟),则他比实际情况早到学校3.3分钟.
≈3.3(分钟),则他比实际情况早到学校3.3分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?
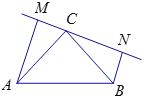
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
 有实根。
有实根。(1)求
 取值范围;
取值范围;(2)若原方程的两个实数根为
 ,且
,且 ,求
,求 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )

A.①②③ B.①②④ C.②③④ D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,
是等边三角形, 是
是 边上的高,点E是
边上的高,点E是 边的中点,点P是
边的中点,点P是 上的一个动点,当
上的一个动点,当 最小时,
最小时, 的度数是( )
的度数是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H, AE=CF,BE=EG。

(1)求证:EF//AC;
(2)求∠BEF大小;
(3)求证:

相关试题

