搜索
【题目】按要求完成下列题目．
（1）求：
+
+
+…+
的值．
对于这个问题，可能有的同学接触过，一般方法是考虑其中的一般项，注意到上面和式的每一项可以写成的形式，而=
﹣
，这样就把一项（分）裂成了两项．
试着把上面和式的每一项都裂成两项，注意观察其中的规律，求出上面的和，并直接写出+++…+
的值．
（2）若
=
+
①求：A、B的值：
②求：
+
+…+的值．
参考答案：
【答案】（1）
；（2）①A和B的值分别是
和﹣；②
．
【解析】
试题（1）根据题目叙述的方法即可求解；
（2）①把等号右边的式子通分相加，然后根据对应项的系数相等可求解；
②根据
=
﹣
把所求的每个分式化成两个分式的差的形式，然后求解.
试题解析：解：（1）
+
+
+…+
=1﹣+﹣
+﹣
+…+
﹣
=1﹣
=；
（2）①∵
+
=
=，
∴
，
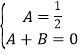解得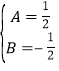
．
∴A和B的值分别是和﹣；
②∵=﹣
=（
﹣
）﹣（﹣
）
∴原式=﹣+﹣+…+﹣
=﹣
=﹣
=．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A（0，6），B（8，0）．点P从A点出发，以每秒1个单位的速度沿AO运动；同时，点Q从O出发，以每秒2个单位的速度沿OB运动，当Q点到达B点时，P、Q两点同时停止运动．
（1）求运动时间t的取值范围；
（2）t为何值时，△POQ的面积最大？最大值是多少？
（3）t为何值时，以点P、0、Q为顶点的三角形与Rt△AOB相似？ -
科目： 来源： 题型：
查看答案和解析>>【题目】2017年中秋节期间，某商城隆重开业，某商家有计划选购甲、乙两种礼盒作为开业期间给予买家的礼品，已知甲礼盒的单价是乙礼盒单价的1.5倍；用600元单独购买甲种礼盒比单独购买乙种礼盒要少10个．
（1）求甲、乙两种礼盒的单价分别为多少元？
（2）若商家计划购买这两种礼盒共40个，且投入的经费不超过1050元，则购买的甲种礼盒最多买多少个？
-
科目： 来源： 题型：
查看答案和解析>>【题目】每年淘宝网都会举办“双十一”购物活动，许多商家都会利用这个契机进行打折让利的促销活动．甲网店销售一件A商品成本为50元，网上标价80元．
（1）“双十一”购物活动当天，甲网店连续两次降价销售A商品吸引买主，问平均每次降价率为多少，才能使这件A商品的利润率为10%？（
≈0.83）
（2）据媒体爆料，有一些淘宝商家在“双十一”购物活动当天，先提高商品的网上标价后再推出促销活动，存在欺诈行为．“双十一”活动之前，乙网店销售A商品的成本、网上标价与甲网店一致，一周可售出60件A商品．在“双十一”购物活动这天，乙网店先将网上标价提高a%，再推出五折销售的促销活动，吸引了大量网购者，乙网店在“双十一”购物活动当天卖出的A商品数量也比原来一周卖出的A商品数量增加了a%，这样“双十一”活动当天乙网店的利润达到了3600元，求乙网店在“双十一”购物活动这天的网上标价为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】感知：如图①，点E在正方形ABCD的BC边上，BF⊥AE于点F，DG⊥AE于点G．可知△ADG≌△BAF.（不要求证明）
拓展：如图②，点B、C在∠MAN的边AM、AN上，点E, F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC,∠1=∠2=∠BAC.求证：△ABE≌△CAF.
应用：如图③，在等腰三角形ABC中，AB=AC，AB＞BC．点D在边B上．CD=2BD.点E, F在线段AD上．∠1=∠2=∠BAC．若△ABC的面积为9，则△ABE与△CDF的面积之和为_________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在下列条件中，不能证明△ABD≌△ACD的是（ ）.
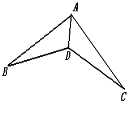
A.BD=DC， AB=AC B.∠ADB=∠ADC，BD=DC
C.∠B=∠C，∠BAD=∠CAD D. ∠B=∠C，BD=DC
-
科目： 来源： 题型：
查看答案和解析>>【题目】课题学习：我们知道二次函数的图象是抛物线，它也可以这样定义：如果一个动点M（x，y）到定点A（0，m）（m＞0）的距离与它到定直线y=﹣m的距离相等，那么动点M形成的图形就是抛物线y=ax2（a＞0）的图象，如图所示．
（1）探究：当x≠0时，a与m有何数量关系？
（2）应用：已知动点M（x，y）到定点A（0，4）的距离与到定直线y=﹣4的距离相等，请写出动点M形成的抛物线的解析式．
（3）拓展：根据抛物线的平移变换，抛物线y=
（x﹣1）2+2的图象可以看作到定点A（ ， ）的距离与它到定直线y=的距离相等的动点M（x，y）所形成的图形．
（4）若点D的坐标是（1，8），在（2）中求得的抛物线上是否存在点P，使得PA+PD最短？若存在，求出点P的坐标，若不存在，请说明理由．
相关试题
