【题目】(1)如图(1),将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图(2)形状拼成一个正方形.
①图(2)中的空白部分的边长是多少?(用含a,b的式子表示)
②观察图(2),用等式表示出![]() ,ab和
,ab和![]() 的数量关系;
的数量关系;

(2)如图所示,在△ABC与△DCB中,AC与BD相交于点E,且∠A=∠D,AB=DC.求证:△ABE≌△DCE;

参考答案:
【答案】(1)①2a-b;②![]() =
=![]() -8ab;(2)见解析
-8ab;(2)见解析
【解析】
(1)①先计算空白正方形的面积,再求边长;
②利用等量关系式S空白=S大正方形-4个S长方形代入即可;
(2)分析题意,根据∠A=∠D,AB=DC以及对顶角就可证明两三角形全等.
(1)①∵图(2)中的空白部分的面积=![]() -4a×2b=4
-4a×2b=4![]() +4ab+
+4ab+![]() -8ab=
-8ab=![]() ,
,
∴图(2)中的空白部分的边长是:2a-b;
②∵S空白=S大正方形-4个S长方形,
∴![]() =
=![]() -4×2a×b,
-4×2a×b,
则![]() =
=![]() -8ab;
-8ab;
(2) 证明: ∵在△ABE和△DCE中,
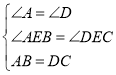
∴△ABE≌△DCE;
-
科目: 来源: 题型:
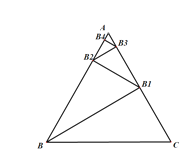
查看答案和解析>>【题目】如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,……Bn-1Bn是△ABn-2Bn-1的高,则B4B5的长是________,猜想Bn-1Bn的长是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,
∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别为多少?

(2)(生活应用题)某公司对一批某一品牌的衬衣的质量抽检结果如下表:

①从这批衬衣中任抽1件是次品的概率约为多少?
②如果销售这批衬衣600件,那么至少需要准备多少件正品衬衣供买到次品的顾客调换?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年年初,在我国湖北等地区爆发了新型冠状病毒引发的肺炎疫情,对此湖北武汉率先采取了“封城”的措施,为了解决武汉市民的生活物资紧缺问题,某省给武汉捐献一批水果和蔬菜共435吨,其中蔬菜比水果多97吨.
(1)求蔬菜和水果各有多少吨?
(2)某慈善组织租用甲、乙两种货车共16辆,已知一辆甲车同时可装蔬菜18吨,水果10吨;一辆乙车同时可装蔬菜16吨,水果11吨;若将这批货物一次性运到武汉,有哪几种租车方案?请你帮忙设计出来.
(3)若甲种货车每辆需付燃油费1600元,乙种货车每辆需付燃油费1200元,应选(2)中的那种方案,才能使所付的燃油费最少?最少的燃油费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(0,8),(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A'处,折痕所在直线交y轴正半轴于点C.

(1)求直线BC的函数表达式;
(2)把直线BC向左平移,使之经过点A',求平移后直线的函数表达式.
相关试题

