【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.

(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π).
参考答案:
【答案】(1)![]() π;(2)
π;(2)![]() π﹣
π﹣![]() .
.
【解析】
试题分析:(1)根据垂径定理求得PD⊥AB,然后根据30°角的直角三角形的性质求得OA=2OD,进而求得OF=![]() OP,根据三角形中位线的性质求得OD=
OP,根据三角形中位线的性质求得OD=![]() BC,从而求得OA=2,然后根据弧长公式即可求得劣弧PC的长;
BC,从而求得OA=2,然后根据弧长公式即可求得劣弧PC的长;
(2)求得OF和PF,然后根据S阴影=S扇形﹣S△OPF即可求得.
解:(1)∵点D是AB的中点,PD经过圆心,
∴PD⊥AB,
∵∠A=30°,
∴∠POC=∠AOD=60°,OA=2OD,
∵PF⊥AC,
∴∠OPF=30°,
∴OF=![]() OP,
OP,
∵OA=OC,AD=BD,
∴BC=2OD,
∴OA=BC=2,
∴⊙O的半径为2,
∴劣弧PC的长=![]() =
=![]() =
=![]() π;
π;
(2)∵OF=![]() OP,
OP,
∴OF=1,
∴PF=![]() =
=![]() ,
,
∴S阴影=S扇形﹣S△OPF=![]() ﹣
﹣![]() ×1×
×1×![]() =
=![]() π﹣
π﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=﹣
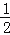 x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.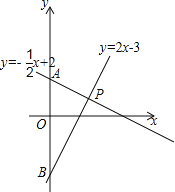
(1)求△PAB的面积;
(2)求证:∠APB=90°;
(3)若在一次函数y=2x﹣3的图象上有一点N,且横坐标为x,连结NA,请直接写出△NAP的面积关于x的函数关系式,并写出相应x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习完一次函数后,小荣遇到过这样的一个新颖的函数:y=|x﹣1|,小荣根据学校函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小荣的探究过程,请补充完成:
(1)列表:下表是y与x的几组对应值,请补充完整.
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
4
2
1
…
(2)描点连线:在平面直角坐标系xOy中,请描出以上表中各对对应值为坐标的点,画出该函数的图象;
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合函数的图象,写出该函数的其他性质(一条即可): .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列定理中,有逆定理的是( )
A. 对顶角相等 B. 同角的余角相等
C. 全等三角形对应角相等 D. 在一个三角形中,等边对等角
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 每一个命题都有逆命题 B. 假命题的逆命题一定是假命题
C. 每一个定理都有逆定理 D. 假命题没有逆命题
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出下列命题的逆命题,并判断逆命题的真假,若是假命题,请举出反例.
(1)若x=y=0,则x+y=0.
(2)等腰三角形的两个底角相等.
相关试题

