【题目】已知一次函数y=﹣![]() x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
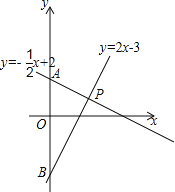
(1)求△PAB的面积;
(2)求证:∠APB=90°;
(3)若在一次函数y=2x﹣3的图象上有一点N,且横坐标为x,连结NA,请直接写出△NAP的面积关于x的函数关系式,并写出相应x的取值范围.
参考答案:
【答案】(1)5;(2)证明见解析;(3)当x>2时,△NAP的面积S=![]() (x﹣2);
(x﹣2);
当x<2时,△NAP的面积S=![]() (2﹣x).
(2﹣x).
【解析】
试题分析:(1)首先解两个一次函数的解析式组成的方程组求得P的坐标,然后求得A和B的坐标,则AB的长即可求得,根据三角形的面积即可求得;
(2)利用勾股定理的逆定理求解;
(3)表示出PN的长,然后根据三角形的面积公式即可求解.
解:(1)根据题意得: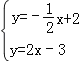 ,
,
解得:![]() ,
,
则P的坐标是(2,1).
在y=﹣![]() x+2中令x=0,解得y=2,则A的坐标是(0,2),
x+2中令x=0,解得y=2,则A的坐标是(0,2),
在y=2x﹣3中令x=0,解得y=﹣3,则B的坐标是(0,﹣3),
则AB=5,
则S△PAB=![]() ×5×2=5;
×5×2=5;
(2)∵PA2=22+(2﹣1)2=5,
BP2=22+(1+3)2=20,
AB2=25,
∴PA2+BP2=AB2,
∴△PAB是直角三角形,∠APB=90°;
(3)N的横坐标是x,则纵坐标是(x,2x﹣3).
则PN=![]() =
=![]() |x﹣2|,
|x﹣2|,
当x>2时,PN=![]() (x﹣2),
(x﹣2),
则△NAP的面积S=![]() PAPN=
PAPN=![]() ×
×![]() ×
×![]() (x﹣2)=
(x﹣2)=![]() (x﹣2);
(x﹣2);
当x<2时,PN=![]() (2﹣x),
(2﹣x),
则△NAP的面积S=![]() PAPN=
PAPN=![]() ×
×![]() ×
×![]() (2﹣x)=
(2﹣x)=![]() (2﹣x).
(2﹣x).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC;②∠EDA=∠B;③OA=
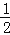 AC;④DE是⊙O的切线,正确的个数是( )
AC;④DE是⊙O的切线,正确的个数是( )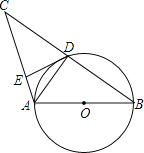
A.1 个 B.2个 C.3 个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(2x+1)(x﹣3)=1的一般形式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形两边长分别是2,4,第三边长为偶数,第三边长为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习完一次函数后,小荣遇到过这样的一个新颖的函数:y=|x﹣1|,小荣根据学校函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小荣的探究过程,请补充完成:
(1)列表:下表是y与x的几组对应值,请补充完整.
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
4
2
1
…
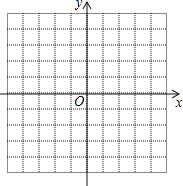
(2)描点连线:在平面直角坐标系xOy中,请描出以上表中各对对应值为坐标的点,画出该函数的图象;
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合函数的图象,写出该函数的其他性质(一条即可): .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.

(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π).
相关试题

