【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD. 
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程x+ ![]() =m的两实根,且tan∠PCD=
=m的两实根,且tan∠PCD= ![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】
(1)证明:∵PQ∥AB,
∴∠ABD=∠BDQ=∠ACD,
∵∠ACD=∠BCD,
∴∠BDQ=∠ACD,
如图1,连接OB,OD,交AB于E,

则∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,
在△OBD中,∠OBD+∠ODB+∠O=180°,
∴2∠ODB+2∠O=180°,
∴∠ODB+∠O=90°,
∴PQ是⊙O的切线
(2)证明:如图2,连接AD,

由(1)知PQ是⊙O的切线,
∴∠BDQ=∠DCB=∠ACD=∠BCD=∠BAD,
∴AD=BD,
∵∠DBQ=∠ACD,
∴△BDQ∽△ACD,
∴ ![]() =
= ![]() ,
,
∴BD2=ACBQ
(3)解:方程x+ ![]() =m可化为x2﹣mx+4=0,
=m可化为x2﹣mx+4=0,
∵AC、BQ的长是关于x的方程x+ ![]() =m的两实根,
=m的两实根,
∴ACBQ=4,由(2)得BD2=ACBQ,
∴BD2=4,
∴BD=2,
由(1)知PQ是⊙O的切线,
∴OD⊥PQ,
∵PQ∥AB,
∴OD⊥AB,由(1)得∠PCD=∠ABD,
∵tan∠PCD= ![]() ,
,
∴tan∠ABD= ![]() ,
,
∴BE=3DE,
∴DE2+(3DE)2=BD2=4,
∴DE= ![]() ,
,
∴BE= ![]() ,
,
设OB=OD=R,
∴OE=R﹣ ![]() ,
,
∵OB2=OE2+BE2,
∴R2=(R﹣ ![]() )2+(
)2+( ![]() )2,
)2,
解得:R=2 ![]() ,
,
∴⊙O的半径为2 ![]()
【解析】(1)根据平行线的性质和圆周角定理得到∠ABD=∠BDQ=∠ACD,连接OB,OD,交AB于E,根据圆周角定理得到∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,根据三角形的内角和得到2∠ODB+2∠O=180°,于是得到∠ODB+∠O=90°,根据切线的判定定理即可得到结论;(2)证明:连接AD,根据等腰三角形的判定得到AD=BD,根据相似三角形的性质即可得到结论;(3)根据题意得到ACBQ=4,得到BD=2,由(1)知PQ是⊙O的切线,由切线的性质得到OD⊥PQ,根据平行线的性质得到OD⊥AB,根据三角函数的定义得到BE=3DE,根据勾股定理得到BE= ![]() ,设OB=OD=R,根据勾股定理即可得到结论.
,设OB=OD=R,根据勾股定理即可得到结论.
【考点精析】关于本题考查的分式方程的解和圆周角定理,需要了解分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.

(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2
 米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)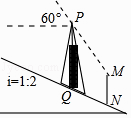
-
科目: 来源: 题型:
查看答案和解析>>【题目】宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=
 .
.
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2=
 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x=
他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x=  ,y=
,y=  .
.
(1)请你帮小明写出中点坐标公式的证明过程;
(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
(3)如图3,点P(2,n)在函数y= x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A坐标为(2,0),以OA为边在第一象限内作等边△OAB,点C为x轴上一动点,且在点A右侧,连接BC,以BC为边在第一象限内作等边△BCD,连接AD交BC于E.

(1)①直接回答:△OBC与△ABD全等吗?
②试说明:无论点C如何移动,AD始终与OB平行;
(2)当点C运动到使AC2=AEAD时,如图2,经过O、B、C三点的抛物线为y1 . 试问:y1上是否存在动点P,使△BEP为直角三角形且BE为直角边?若存在,求出点P坐标;若不存在,说明理由;
(3)在(2)的条件下,将y1沿x轴翻折得y2 , 设y1与y2组成的图形为M,函数y= x+
x+  m的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
m的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是 .
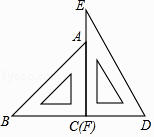
相关试题

