【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
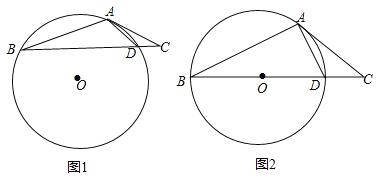
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
参考答案:
【答案】(1)证明见解析;(2)22.5°.
【解析】
试题分析:(1)连接AO,延长AO交⊙O于点E,则AE为⊙O的直径,连接DE,由已知条件得出∠ABC=∠CAD,由圆周角定理得出∠ADE=90°,证出∠AED=∠ABC=∠CAD,求出EA⊥AC,即可得出结论;
(2)由圆周角定理得出∠BAD=90°,由角的关系和已知条件得出∠ABC=22.5°,由(1)知:∠ABC=∠CAD,即可得出结果.
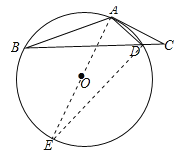
试题解析:(1)连接AO,延长AO交⊙O于点E,则AE为⊙O的直径,连接DE,如图所示:
∵∠ABC:∠ACB:∠ADB=1:2:3,∠ADB=∠ACB+∠CAD,∴∠ABC=∠CAD,∵AE为⊙O的直径,∴∠ADE=90°,∴∠EAD=90°﹣∠AED,∵∠AED=∠ABD,∴∠AED=∠ABC=∠CAD,∴∠EAD=90°﹣∠CAD,即∠EAD+∠CAD=90°,∴EA⊥AC,∴AC是⊙O的切线;
(2)∵BD是⊙O的直径,∴∠BAD=90°,∴∠ABC+∠ADB=90°,∵∠ABC:∠ACB:∠ADB=1:2:3,∴4∠ABC=90°,∴∠ABC=22.5°,由(1)知:∠ABC=∠CAD,∴∠CAD=22.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+x﹣1经过点P(m,5),则代数式m2+m+2018的值为( )
A. 2021B. 2022C. 2023D. 2024
-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次不等式解应用题的关键就是找出题中的,并将它转化为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把(-5)-(+3)-(-7)+(-2)写成省略加号和括号的形式,正确的是( )
A. -5-3+7-2 B. 5-3-7-2 C. 5-3+7-2 D. 5+3-7-2
-
科目: 来源: 题型:
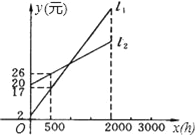
查看答案和解析>>【题目】如图所示,l1和l2分别表示一种白炽灯和一种节能灯的费用y(元)与照明时间x(小时)的函数关系图象,假设两种灯的使用寿命都是2000小时,照明效果一样.(费用=灯的售价+电费)
(1)根据图象分别求出l1,l2的函数关系式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣3x=0的根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=(a-3)x2-2有最低点,那么a的取值范围是________.
相关试题

