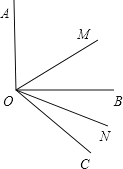
【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?
参考答案:
【答案】(1)45°(2)![]() (3)45°(4)∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
(3)45°(4)∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
【解析】(1)先求出∠MOC的度数:(90+30)÷2=60°,∠CON的度数是:30÷2=15°,然后用∠MOC的度数减去∠CON的度数即可得出∠MON的度数.
(2)根据问题(1)的解题思路把∠AOB的度数用字母a代替即可.
(3)根据问题(1)的解题思路把∠BOC的度数用字母![]() 代替即可.
代替即可.
(4)根据(1)(2)(3)的得数可知:∠MON的度数是始终是∠AOB的度数的一半》
解:(1)因为OM平分∠AOC,
所以∠MOC=![]() ∠AOC.
∠AOC.
又因为ON平分∠BOC,
所以∠NOC=![]() ∠BOC.
∠BOC.
所以∠MON=∠MOC-∠NOC=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)=![]() ∠AOB.
∠AOB.
又因为∠AOB=90°,所以∠MON=45°.
(2)当∠AOB=α,其他条件不变时,∠MON=![]() .
.
(3)当∠BOC=β,其他条件不变时,∠MON=45°.
(4)分析(1)(2)(3)的结果和(1)的解答过程可知:∠MON的大小总等于∠AOB的一半,与锐角∠BOC的大小无关.
“点睛”本题考查了组合角中某个角的度数的求解,根据是明确各角之间的联系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知线段
 ,点
,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,如图1所示.
,如图1所示.
(1)平移线段

 到线段
到线段
 ,使点
,使点 的对应点为,点
的对应点为,点 的对应点为
的对应点为 ,若点
,若点 的坐标为
的坐标为 ,求点
,求点 的坐标;
的坐标; (2)平移线段

 到线段
到线段
 ,使点
,使点 在
在 轴的正半轴上,点
轴的正半轴上,点 在第二象限内(
在第二象限内( 与
与 对应,
对应,  与
与 对应),连接
对应),连接 如图2所示.若
如图2所示.若 表示△BCD的面积),求点
表示△BCD的面积),求点 、
、 的坐标;
的坐标; (3)在(2)的条件下,在
 轴上是否存在一点
轴上是否存在一点 ,使
,使 表示△PCD的面积)?若存在,求出点
表示△PCD的面积)?若存在,求出点 的坐标; 若不存在,请说明理由.
的坐标; 若不存在,请说明理由. -
科目: 来源: 题型:
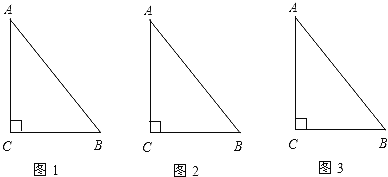
查看答案和解析>>【题目】有一块直角三角形的绿地,量得两直角边长分别为6m和8m,现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2008年8月第29届奥运会将在北京开幕,5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2008年8月8日20时应是( )
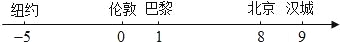
A. 伦敦时间2008年8月8日11时
B. 巴黎时间2008年8月8日13时
C. 纽约时间2008年8月8日5时
D. 汉城时间2008年8月8日19时
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刘对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.
请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分的图形补充完整;
(2)在图2中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数;
(3)观察图1和图2,你能得出哪些结论(只要写出一条结论).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
相关试题

