【题目】如图,在ABCD中,AD=2AB,点F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中一定成立的是____.(把所有正确结论的序号都填在横线上)

①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
参考答案:
【答案】①②④
【解析】试题解析:①∵F是AD的中点,
∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=![]() ∠BCD,故此选项正确;
∠BCD,故此选项正确;
延长EF,交CD延长线于M,
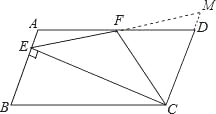
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
 ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故此选项正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,BC=24cm,P、Q、M、N分别从A、B、C、D出发,沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止、已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm,
(1)当x为何值时,点P、N重合;
(2)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】人体中成熟的红细胞的平均直径为0.000 007 7 m,用科学记数法表示为( )
A.7.7×10-5 mB.77×10-6 m
C.77×10-5 mD.7.7×10-6 m
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个事件,事件A:掷一次骰子,向上的一面是3;事件B:篮球队员在罚球线上投篮一次,投中.则( )
A.只有事件A是随机事件;B.只有事件B是随机事件
C.事件A和B都是随机事件;D.事件A和B都不是随机事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】贵州FAST望远镜是目前世界第一大单口径射电望远镜,反射面总面积约250000m2 , 这个数据用科学记数法可表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列各题.
(1)先化简,再求值:
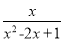 ÷
÷ ,其中x=
,其中x= +1.
+1.(2)分解因式:8(x2-2y2)-x(7x+y)+xy.
(3)解不等式
 ≤
≤ -1,并把解集表示在数轴上.
-1,并把解集表示在数轴上.
(4)解不等式组
 并将解集在数轴上表示出来.
并将解集在数轴上表示出来.
(5)解方程:
 +
+ =4.
=4. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑比购买3台学习机多600元,购买2台平板电脑和3台学习机共需8400元.
(1)求购买1台平板电脑和1台学习机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168000元,且购买学习机的台数不超过购买平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
相关试题

