【题目】如图,矩形ABCD中,AB=10,BC=8,P为AD上一点,将△ABP沿BP翻折至△EBP(点A落在点E处),PE与CD相交于点O,且OE=OD,则DP的长为( )

A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
参考答案:
【答案】A
【解析】
由折叠的性质得出EP=AP,∠E=∠A=90°,证△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,在直角三角形BCG中,由勾股定理得BC2+CG2=BG2,即82+(10-x)2=(x+2)2,再求得x.
如图所示,由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=10,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=8-x,DG=PE=x,求出GC=10-x、BG=10-(8-x),根据勾股定理BC2+CG2=BG2,
得出方程82+(10-x)2=(x+2)2,解方程即可得到x=![]() ,即AP的长为
,即AP的长为![]() .
.
所以,PD=AD-AP=8-![]() =
=![]() .
.
故选:A
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装商预测一种应季衬衫能畅销市场,就用8000元购进一批衬衫,面市后果然供不应求,服装商又用17600元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了8元.商家销售这种衬衫时每件定价都是100元,最后剩下10件按8折销售,很快售完.在这两笔生意中,商家共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列方程的特征及其解的特点.
①x+
 =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;②x+
 =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;③x+
 =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.解答下列问题:
(1)请你写出一个符合上述特征的方程为________,其解为________;
(2)根据这类方程的特征,写出第n个方程为________,其解为________;
(3)请利用(2)的结论,求关于x的方程x+
 =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】取一个自然数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明.但举例验证都是正确的.例如:取自然数5.最少经过下面5步运算可得1,即:5
 16
16  8
8  4
4  2
2  1,如果自然数m最少经过7步运算可得到1,则所有符合条件的m的最小值为 .
1,如果自然数m最少经过7步运算可得到1,则所有符合条件的m的最小值为 . -
科目: 来源: 题型:
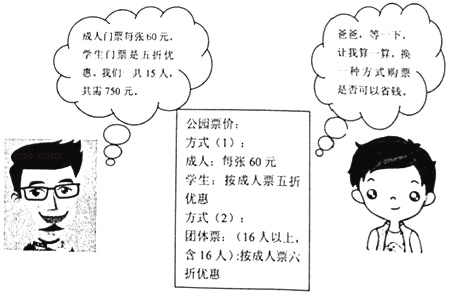
查看答案和解析>>【题目】在”元旦“期间,罗山县尚文学校七一班的小明、小亮等同学随家长一同到信阳波尔登森林公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)小明他们一共去了几个成人,几个学生?
(2)小明用所学的数字知识很快算出了哪种方式更省钱,你知道吗?请写出你的推算过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩被分别绘制成如下两个统计图:
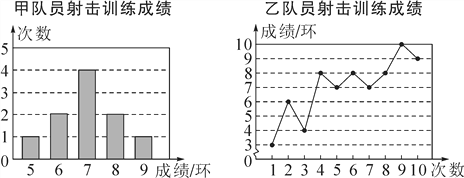
根据以上信息,整理分析数据如下:
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
4.2
(1)则表格中a,b的值分别是a=________,b=________;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
相关试题

