【题目】钝角三角形ABC中,∠BAC>90°,∠ACB=α,∠ABC=β,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE. 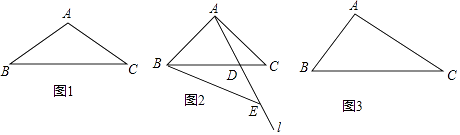
(1)若AB=AC,点E在AD延长线上. 当α=30°,点D恰好为BE中点时,补全图1,直接写出∠BAE=°,
∠BEA=°;
(2)如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
(3)如图3,若AB<AC,∠BEA的度数与(1)中②的结论相同,直接写出∠BAE,α,β满足的数量关系.
参考答案:
【答案】
(1)60;30
(2)解:如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N.
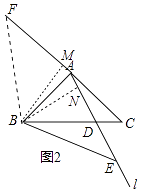
∵AB=AC,
∴∠ABC=∠C=α,
∴∠MAB=2α,∵∠BAN=2α,
∴∠BAM=∠BAN,
∴BM=BN,
在Rt△BMF和Rt△BNE中,
![]() ,
,
∴Rt△BMF≌Rt△BNE.
∴∠BEA=∠F,
∵BF=BC,
∴∠F=∠C=α,
∴∠BEA=α
(3)解:结论:∠BAE=α+β.理由如下,
如图3中,连接EC,
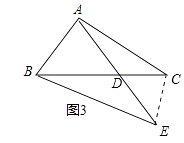
∵∠ACD=∠BED=α,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠ADB=∠CDE,
,∵∠ADB=∠CDE,
∴△ADB∽△CDE,
∴∠BAD=∠DCE,
∠ABD=∠DEC=β,
∵BC=BE,
∴∠BCE=∠BEC,
∴∠BAE=∠BEC=∠BEA+∠DEC=α+β
【解析】解:(1)补全图1,如图所示. 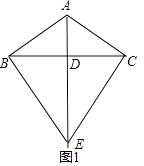
∵AB=AC,BD=DC,
∴AE⊥BC,
∴EB=EC,∠ADB=90°,
∵∠ABC=30°,
∴∠BAE=60°
∵BC=BE,
∴△BCE是等边三角形,∠DEB=∠DEC,
∴∠BEC=60°,∠BEA=30°
所以答案是60,30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
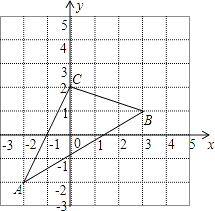
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2﹣2x+k=0有实数根,则k的取值范围是( )
A. k<1B. k<4C. k≤1D. k≤4
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m是方程x2+x﹣1=0的一个根,则代数式2019﹣m2﹣m的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形如果是轴对称图形,那么它的边数与对称轴的条数之间存在联系吗?
(1)以凸六边形为例,如果这个凸六边形是轴对称图形,那么它可能有条对称轴;
(2)凸五边形可以恰好有两条对称轴吗?如果存在请画出图形,并用虚线标出两条对称轴;否则,请说明理由;
(3)通过对(1)中凸六边形的研究,请大胆猜想,一个凸多边形如果是轴对称图形,那么它的边数与对称轴的条数之间的联系是: . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD、过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)求证:△FDB∽△FAD;
(3)如果⊙O的半径为5,sin∠ADE=
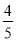 ,求BF的长.
,求BF的长.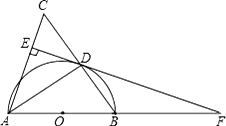
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,计算正确的是( )
A.(15x2y﹣5xy2)÷5xy=3x﹣5y
B.98×102=(100﹣2)(100+2)=9996
C.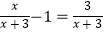
D.(3x+1)(x﹣2)=3x2+x﹣2
相关试题

