【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P,Q两点停止运动.
(1)AC= cm,BC= cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,P与Q第一次相遇;
(4)当t为何值时,PQ=1cm.
![]()
参考答案:
【答案】(1)4,8;(2) ![]() ;(3)2;(4)t为
;(3)2;(4)t为![]() 或
或![]() 或
或![]() 时,PQ=1cm.
时,PQ=1cm.
【解析】
(1)根据AB=AC+BC=12cm,BC=2AC,即可求出AC=4cm,BC=8cm;
(2)用含t的代数式分别表示AP、PQ,根据AP=PQ列出方程,求解即可;
(3)当P与Q第一次相遇时,AP=AC+CQ,依此列出关于t的方程,求解即可;
(4)当PQ=1cm时,从点P的运动方向可分两种情况进行讨论:(Ⅰ)当点P从点A出发向点B运动时,又分P追上Q前与P追上Q后两种情况;(Ⅱ)当点P到达点B后立即返回时,由于当点P与点Q第二次重合时,P,Q两点停止运动,所以只有点P与Q相遇前一种情况.
(1)∵AB=AC+BC=12cm,BC=2AC,
∴AC+2AC=12,
∴AC=4cm,BC=8cm.
(2)当AP=PQ时,AP=3t,PQ=AC+CQ-AP=4+t-3t,
即3t=4+t-3t,解得t=![]() .
.
所以当t=![]() 时,AP=PQ;
时,AP=PQ;
(3)当P与Q第一次相遇时,AP=AC+CQ,
即3t=4+t,解得t=2.
所以当t=2时,P与Q第一次相遇;
(4)(Ⅰ)当点P从点A出发向点B运动时,
P追上Q前,由PQ=AC+CQ-AP=1,可得4+t-3t=1,解得t=![]() ;
;
P追上Q后,由PQ=AP-(AC+CQ)=1,可得3t-(4+t)=1,解得t=![]() ;
;
(Ⅱ)当点P到达点B后立即返回时,点P与Q相遇前.
∵AB+BP=3t,
∴BP=3t-12.
∵PQ=BC-BP-CQ=1,
∴8-(3t-12)-t=1,
解得t=![]() .
.
综上所述,当t为![]() 或
或![]() 或
或![]() 时,PQ=1cm.
时,PQ=1cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣
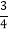 x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,则过B、C两点直线的解析式是_____.
x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,则过B、C两点直线的解析式是_____.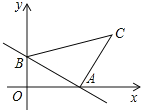
-
科目: 来源: 题型:
查看答案和解析>>【题目】坐标平面内有4个点A(0,2),B(-2,0),C(1,-1),D(3,1).
(1)建立坐标系,描出这4个点;
(2)顺次连接A,B,C,D,组成四边形ABCD,求四边形ABCD的面积.
(3)线段AB,CD有什么关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=
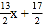 ,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为_____.
,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为_____.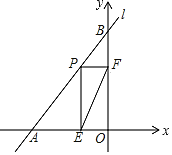
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车计费标准如下:行驶路程不超过3千米时,收费8元;行驶路程超过3千米的部分,按每千米1.60元计费.
(1)求出租车收费y(元)与行驶路程x(千米)之间的函数关系式;
(2)若某人一次乘出租车时,付出了车费14.40元,求他这次乘坐了多少千米的路?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E、F分别是AD、CD的中点,EF与BD相交于点M,若△DEM的面积为1,则ABCD的面积为 .
相关试题

