【题目】如图,一次函数![]() 的图像分别与x轴、y轴交于点A、B,以线段AB为腰在第二象限内作等腰Rt△ABC,∠BAC=90°.
的图像分别与x轴、y轴交于点A、B,以线段AB为腰在第二象限内作等腰Rt△ABC,∠BAC=90°.
(1)直接写出A、B两点的坐标,并求线段AB的长;
(2)求过B、C两点的直线的函数表达式.

参考答案:
【答案】(1)A(-3,0),B(0,2),AB=![]() ;(2)y=-0.2x+2;
;(2)y=-0.2x+2;
【解析】
(1)先根据一次函数的解析式把x=0或y=0代入,即可求出A、B两点的坐标,根据勾股定理即可求出AB的长;
(2)作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,故可得出C点坐标,再用待定系数法即可求出直线BC的解析式.
解:(1)∵一次函数![]() 中,
中,
令x=0得:y=2;
令y=0,解得x=-3,
∴A的坐标是(-3,0),B的坐标是(0,2),
∴AB=![]() ;
;
(2)如图,作CD⊥x轴于点D.

∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO.
在△ABO与△CAD中,
 ,
,
∴△ABO≌△CAD(AAS),
∴OB=AD=2,OA=CD=3,OD=OA+AD=5,
则C的坐标是(-5,3),
设直线BC的解析式是y=kx+b,
根据题意得:![]() ,
,
解得:k=-0.2,b=2,
∴直线BC的解析式是y=-0.2x+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
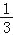 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
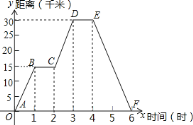
查看答案和解析>>【题目】小明同学骑自行车去滨海港郊游,中途休息了一段时间。如图表示他离家的距离y(千米)与所用的时间s(小时)之间关系的函数图像
(1)根据图像回答:小明家离滨海港 千米,小明到达滨海港时用了 小时;
(2)直线CD的函数解析式为 ;
(3)小明出发几小时,离家12千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④后面的横线上写出相应的等式:

①1=12;②1+3=22;③1+3+5=32;④ ;⑤1+3+5+7+9=52;…
(2)请写出第n个等式;
(3)利用(2)中的等式,计算21+23+25+…+99.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长都为a的正方形内分别排列着一些大小相等的圆.

(1)根据图中的规律,第4个正方形内圆的个数是 ,第n个正方形内圆的个数是 .
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a的代数式分别表示第1个正方形中和第3个正方形中阴影部分的面积.(结果保留π)
②若a=10,请直接写出第2014个正方形中阴影部分的面积 .(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据“算法”的约定:在数值转换机中,输入或输出的值写在“平行四边形”框内,计算程序(或步骤)写在“长方形”框内,菱形框则用于对结果作出是否符合要求的判定.因此画数值转换机必须注意框图的选择.
(1)如图,当输入数字为1时,数值转换机输出的结果为 ;
(2)嘉悦的爸爸存入1年期的定期储蓄10000元(假定1年期定期储蓄的年利率为4%)到期后本息和(本金和利息的和)自动转存1年期的定期储蓄.请画出数值转换机,并求出转存几次就能使本息和超过11000元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )

A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
相关试题

