【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.
(1)若∠F=40°,求∠A的度数;
(2)若AB=10,BC=16,CE⊥AD,求ABCD的面积.
参考答案:
【答案】
(1)
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠AEB=∠CBF,∠ABE=∠F=40°,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠AEB=∠ABE=40°,
∴∠A=180°﹣40°﹣40°=100°
(2)
解:∵∠AEB=∠ABE,
∴AE=AB=10,
∵四边形ABCD是平行四边形,
∴AD=BC=16,CD=AB=10,
∴DE=AD﹣AE=6,
∵CE⊥AD,
∴CE=8,
∴ABCD的面积=ADCE=16×8=128
【解析】(1)由平行四边形的性质和已知条件得出∠AEB=∠CBF,∠ABE=∠F=40°,证出∠AEB=∠ABE=40°,由三角形内角和定理求出结果即可;(2)求出DE,由勾股定理求出CE,即可得出结果.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;
③△ACN≌△ABM;④CD=DN.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )
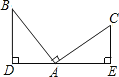
A. AD=AE B. AB=AC C. BD=AE D. AD=CE
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则实数k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(2,y1)、B(3,y2)是二次函数y=x2﹣2x+m的图象上两点,则y1与y2的大小关系为y1_____y2(填“>”、“<”、“=”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数a的平方根是2x﹣1和5﹣x,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数
 的图象和矩形ABCD在第一象限,AD平行于
的图象和矩形ABCD在第一象限,AD平行于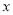 轴,且AB=2,AD=4,点A的坐标为(2,6).
轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标.
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
相关试题

