【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣![]() x+
x+![]() 与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
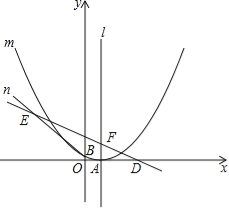
(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2﹣
x2﹣![]() x+1;(2)点P坐标为(3,
x+1;(2)点P坐标为(3,![]() );(3)点Q坐标为(9,4)或(15,16).
);(3)点Q坐标为(9,4)或(15,16).
【解析】试题分析:(1)抛物线顶点在x轴上则可得出顶点纵坐标为0,将解析式进行配方就可以求出a的值,继而得出函数解析式;(2)作出B点关于l的对称点B′,连接EB′交l于点P,如图所示,,三角形BEP为顶点的三角形的周长最小,再求出直线B′E的解析式,进而得出P点坐标;(3)先求出直线FD的解析式,结合以线段FQ为直径的圆恰好经过点D这个条件,明确∠FDG=90°,得出直线DG解析式的k值与直线FD解析式的k值乘积为﹣1,利用D点坐标求出直线DG解析式,将点Q坐标用抛物线解析式表示后代入DG直线解析式可求出点Q坐标.
试题解析:(1)∵抛物线y=ax2﹣6ax+c(a>0)的顶点A在x轴上
∴配方得y=a(x﹣3)2﹣9a+1,则有﹣9a+1=0,解得a=![]()
∴A点坐标为(3,0),抛物线m的解析式为y=![]() x2﹣
x2﹣![]() x+1;
x+1;
(2)∵点B关于对称轴直线x=3的对称点B′为(6,1)
∴连接EB′交l于点P,如图所示

设直线EB′的解析式为y=kx+b,把(﹣7,7)(6,1)代入得
![]() 解得
解得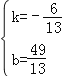 ,
,
则函数解析式为y=﹣![]() x+
x+![]()
把x=3代入解得y=![]() ,
,
∴点P坐标为(3,![]() );
);
(3)∵y=﹣![]() x+
x+![]() 与x轴交于点D,
与x轴交于点D,
∴点D坐标为(7,0),
∵y=﹣![]() x+
x+![]() 与抛物线m的对称轴l交于点F,
与抛物线m的对称轴l交于点F,
∴点F坐标为(3,2),
求得FD的直线解析式为y=﹣![]() x+
x+![]() ,若以FQ为直径的圆经过点D,可得∠FDQ=90°,则DQ的直线解析式的k值为2,
,若以FQ为直径的圆经过点D,可得∠FDQ=90°,则DQ的直线解析式的k值为2,
设DQ的直线解析式为y=2x+b,把(7,0)代入解得b=﹣14,则DQ的直线解析式为y=2x﹣14,
设点Q的坐标为(a,![]() ),把点Q代入y=2x﹣14得
),把点Q代入y=2x﹣14得
![]() =2a﹣14
=2a﹣14
解得a1=9,a2=15.
∴点Q坐标为(9,4)或(15,16).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“掷一枚骰子,出现点数大于4”是_____事件.(填“必然”“不可能”或“随机”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中正方形具有而矩形不具有的是( )
A. 对边相等 B. 对角线相等
C. 四个角都是直角 D. 对角线互相垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )

A.2个 B.3个 C. 4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,EF//AD,∠1=∠2,∠BAC=70°,请将求∠AGD 的过程补充完整.

解:∵EF//AD
∴∠2= ( )
∵∠1=∠2 ∴∠1=∠3 ( )
∴AB//
 ( )
( )∴∠BAC+ =180° ( )
∵∠BAC=70° ∴∠AGD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数为 度。

-
科目: 来源: 题型:
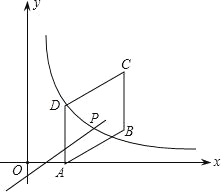
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=
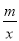 (x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
(x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:①反比例函数的解析式是y1=
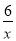 ;
;②一次函数y2=kx+3-3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3-3k的图象经过点C,当x>
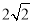 时,y1<y2;
时,y1<y2;④对于一次函数y2=kx+3-3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是
 <a<3.
<a<3.其中正确的是( )
A.①③ B.②③ C.②④ D.③④
相关试题

