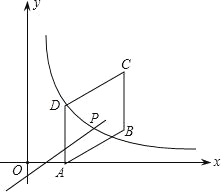
【题目】如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=![]() (x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
(x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
①反比例函数的解析式是y1=![]() ;
;
②一次函数y2=kx+3-3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3-3k的图象经过点C,当x>![]() 时,y1<y2;
时,y1<y2;
④对于一次函数y2=kx+3-3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是![]() <a<3.
<a<3.
其中正确的是( )
A.①③ B.②③ C.②④ D.③④
参考答案:
【答案】D.
【解析】
试题解析:①∵四边形ABCD是平行四边形,
∴AD=BC,
∵B(6,2),C(6,6),
∴BC⊥x轴,AD=BC=4,
而A点坐标为(2,0),
∴点D的坐标为(2,4),
∵反比例函数y1=![]() (x>0)的函数图象经过点D(2,4),
(x>0)的函数图象经过点D(2,4),
∴4=![]() ,
,
∴m=8,
∴反比例函数的解析式为y=![]() ,①不正确;
,①不正确;
②当x=6时,y=kx+3-3k=6k+3-3k=3k+3≠6,
∴一次函数y=kx+3-3k(k≠0)的图象不一定过点C,②不正确;
③∵一次函数y2=kx+3-3k的图象经过点C,
∴6=6k+3-3k,解得:k=1.
∴y2=x.
联立![]() ,解得:
,解得: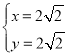 或
或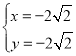 (舍去).
(舍去).
结合函数图象即可得出:
当x>![]() 时,y1<y2,③成立;
时,y1<y2,③成立;
④∵一次函数y2=kx+3-3k(k≠0),y随x的增大而增大,
∴k>0,
∴交点P在第一象限,
∴点P横坐标a的取值范围是![]() <a.
<a.
将x=3带入到反比例函数y=![]() 中,得:y=
中,得:y=![]() .
.
又∵一次函数y2=kx+3-3k(k≠0)恒过点(3,3),点(3,![]() )在(3,3)的下方,
)在(3,3)的下方,
即点P应该在点(3,![]() )的左方,
)的左方,
∴点P横坐标a的取值范围是a<3.
即④正确.
综上可知:③④正确,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣
 x+
x+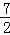 与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).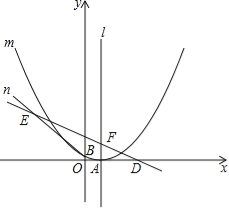
(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,EF//AD,∠1=∠2,∠BAC=70°,请将求∠AGD 的过程补充完整.

解:∵EF//AD
∴∠2= ( )
∵∠1=∠2 ∴∠1=∠3 ( )
∴AB//
 ( )
( )∴∠BAC+ =180° ( )
∵∠BAC=70° ∴∠AGD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数为 度。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a与b互为相反数且都不为零,n为正整数,则下列两数互为相反数的是( )
A. a2n-1与-b2n-1 B. a2n-1与b2n-1 C. a2n与b2n D. an与bn
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.2.5微米等于0.0000025米,把0.000 002 5用科学记数法表示为 .
相关试题

