【题目】阅读资料:我们把顶点在圆上,并且一边和圆相交、另一边和圆相切的角叫做弦切角,如下左图∠ABC所示。
同学们研究发现:P为圆上任意一点,当弦AC经过圆心O时,且AB切⊙O于点A,此时弦切角∠CAB=∠P(图甲)
证明:∵AB切⊙O于点A, ∴∠CAB=90°, 又∵AC是直径, ∴∠P=90° ∴∠CAB=∠P

问题拓展:若AC不经过圆心O(如图乙),该结论:弦切角∠CAB=∠P还成立吗?
请说明理由。
知识运用:如图,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F。 求证:EF∥BC。

参考答案:
【答案】(1)成立;(2)证明见解析.
【解析】试题分析:问题拓展:首先连接AO并延长交⊙O于点D,连接CD,由圆周角定理可得∠D=∠P,又由AD是直径,AB切圆于点A,易证得∠CAB=∠CAD,继而证得结论;
知识运用:连接DF,AD是△ABC中∠BAC的平分线,⊙O与BC切于点D,可得∠FDC=∠EAD,又由圆周角定理可得∠EAD=∠EFD,继而证得结论.
试题解析:问题拓展:成立.
如图3,连接AO并延长交⊙O于点D,连接CD,
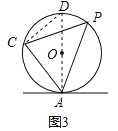
则∠D=∠P,
∵AD是直径,
∴∠D+∠CAD=90°,
又∵AB切圆于点A,
∴∠CAB+∠CAD=90°,
∴∠CAB=∠CAD,
而∠CAD=∠P,
∴∠CAB=∠P;
知识运用:如图4,连接DF,
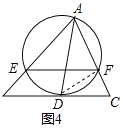
∵AD是△ABC中∠BAC的平分线,
∴∠EAD=∠DAC,
∵⊙O与BC切于点D,
∴∠FDC=∠DAC,
∴∠FDC=∠EAD,
∵在⊙O中∠EAD=∠EFD,
∴∠FDC=∠EFD,
∴EF∥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程,其中可用公理“两点之间,线段最短”来解释的现象有( )
A.①②
B.①③
C.②④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.对顶角相等B.内错角相等C.锐角相等D.同位角相等
-
科目: 来源: 题型:
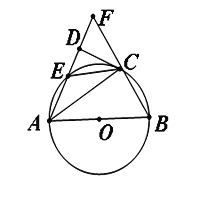
查看答案和解析>>【题目】如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,
(1)求证:直线CD是⊙O的切线.
(2)求证:△FEC是等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某闭合电路中,其两端电压恒定,电流I(A)与电阻R()图像如图所示,回答问题:
(1)写出电流I与电阻R之间的函数解析式。
(2)如果一个用电器的电阻为5 ,其允许通过的最大电流是1A,那么这个用电器接在这个闭合电路中,会不会烧毁?说明理由。
(3)若允许的电流不超过4A时,那么电阻R的取值应该控制在什么范围?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=ax+b的图象经过点A(1,3)且与y=2x-3 平行.
(1)求出a,b.写出y 与x 的函数关系;
(2)求当x=-2 时,y的值,当y=10 时,x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2x(a﹣b)﹣(b﹣a)
相关试题

