【题目】智能折叠电动车是在传统电动车的基础上,根据消费者需求生产的一种新型电动车.某智能折叠电动车公司计划每周生产1400辆,平均每天生产200辆.由于各种原因实际每天生产量与计划每天生产量相比有出入.下表是某周智能折叠电动车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆)

星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
生产情况 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产智能折叠电动车_______辆;
(2)产量最多的一天比产量最少的一天多生产________辆;
(3)若该公司实行按生产的智能折叠电动车数量的多少计工资,即计件工资制.如果每生产一辆智能折叠电动车可得人民币60元,那么该公司工人这一周的工资总额是多少元?
参考答案:
【答案】(1)599辆;(2)26辆;(3)84540元.
【解析】
(1)根据表格中的数据求出前三天生产的总量即可;
(2)求出每天的产量,找出最大比最少的多生产的量即可;
(3)算出一周内总共生产的电动车的数量,然后再乘60,即得到该公司工人这一周的工资总额.
解:(1) “+”表示实际每天比计划每天多生产,“﹣”表示实际每天比计划每天少生产,
故第一天实际生产205辆,
第二天实际生产198辆,
第三天实际生产196辆,
∴前三天共生产智能折叠电动车为:205+198+196=599辆
故答案为:599辆.
(2)一周每天的产量分别是:205,198,196,213,190,216,191
故产量最多的一天比产量最少的一天多生产216-190=26辆.
故答案为:26辆.
(3)一周生产电动车的总量数为:205+198+196+213+190+216+191=1409辆
故一周工人工资的总费用为:1409×60=84540元.
故答案为:84540元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
(1)求出所抽取的学生人数,并把条形统计图补充完整;
(2)样本中喜欢B项目的人数百分比是 ,其所在扇形统计图中的圆心角的度数是 ;
(3)已知该校有1 000人,根据样本估计全校喜欢跳绳的人数是多少?


图甲 图乙
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式组
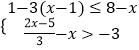 的最小整数解为a,最大整数解为b,则ba=( )
的最小整数解为a,最大整数解为b,则ba=( )
A.
B.﹣8
C.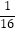
D.16 -
科目: 来源: 题型:
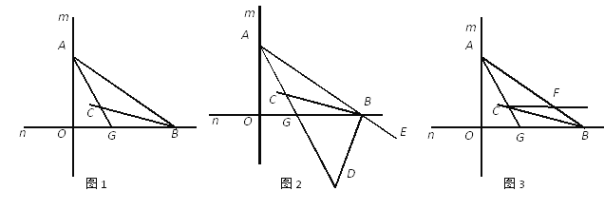
查看答案和解析>>【题目】如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)求∠ACB的大小;
(2)如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;
(3)如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料并完成任务.

莱昂哈德·欧拉是18世纪数学界最杰出的人物之一,瑞士著名的数学家、物理学家,他不但为数学界作出贡献,更把整个数学推至物理的领域;同时,也是数学史上研究成果最多的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学等的课本,《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作.因此,被称为历史上最伟大的两位数学家之一(另一位是卡尔·弗里德里克·高斯).在数学成就上,欧拉最先把关于
 的多项式用记号
的多项式用记号 的形式来表示(
的形式来表示( 可用其他字母代替,但不同的字母表示不同的多项式),例如
可用其他字母代替,但不同的字母表示不同的多项式),例如 ,当
,当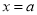 时,多项式的值用
时,多项式的值用 来表示,即
来表示,即 ;当
;当 时,多项式的值用
时,多项式的值用 来表示,记为
来表示,记为 .
.任务:
已知
 ;
; .
.请你根据材料中代入求值的方法解决下列问题:
(1)求
 的值;
的值;(2)求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
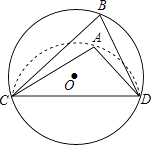
A.110°
B.70°
C.60°
D.55° -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
阅读理解:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如:
在数轴上,有理数3与1对应的两点之间的距离为
 ;
;在数轴上,有理数3与-2对应的两点之间的距离为
 ;
;在数轴上,有理数-3与-2对应的两点之间的距离为
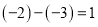 .
.解决问题:如图所示,已知点
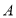 表示的数为-3,点
表示的数为-3,点 表示的数为-1,点
表示的数为-1,点 表示的数为2.
表示的数为2.
(1)点
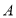 和点
和点 之间的距离为______.
之间的距离为______.(2)若数轴上动点
 表示的数为
表示的数为 ,当
,当 时,点
时,点 和点
和点 之间的距离可表示为______;当
之间的距离可表示为______;当 时,点
时,点 和点
和点 之间的距离可表示为______.
之间的距离可表示为______.(3)若数轴上动点
 表示的数为
表示的数为 ,点
,点 在点
在点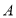 和点
和点 之间,点
之间,点 和点
和点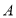 之间的距离表示为
之间的距离表示为 ,点
,点 和点
和点 之间的距离表示为
之间的距离表示为 ,求
,求 (用含
(用含 的代数式表示并进行化简)
的代数式表示并进行化简)(4)若数轴上动点
 表示的数为-2,将点
表示的数为-2,将点 向右移动19个单位长度,再向左移动23个单位长度终点为
向右移动19个单位长度,再向左移动23个单位长度终点为 ,那么
,那么 ,
, 两点之间的距离是______.
两点之间的距离是______.
相关试题

