【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
参考答案:
【答案】
(1)
解:∵抛物线的对称轴x=1,B(3,0),
∴A(﹣1,0)
∵抛物线y=ax2+bx+c过点C(0,3)
∴当x=0时,c=3.
又∵抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0)
∴ ![]() ,
,
∴ ![]()
∴抛物线的解析式为:y=﹣x2+2x+3
(2)
解:∵C(0,3),B(3,0),
∴直线BC解析式为y=﹣x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4)
∵对于直线BC:y=﹣x+1,当x=1时,y=2;将抛物线L向下平移h个单位长度,
∴当h=2时,抛物线顶点落在BC上;
当h=4时,抛物线顶点落在OB上,
∴将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),
则2≤h≤4
(3)
解:设P(m,﹣m2+2m+3),Q(﹣3,n),
①当P点在x轴上方时,过P点作PM垂直于y轴,交y轴与M点,过B点作BN垂直于MP的延长线于N点,如图所示:
∵B(3,0),
∵△PBQ是以点P为直角顶点的等腰直角三角形,
∴∠BPQ=90°,BP=PQ,
则∠PMQ=∠BNP=90°,∠MPQ=∠NBP,
在△PQM和△BPN中, 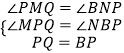 ,
,
∴△PQM≌△BPN(AAS),
∴PM=BN,
∵PM=BN=﹣m2+2m+3,根据B点坐标可得PN=3﹣m,且PM+PN=6,
∴﹣m2+2m+3+3﹣m=6,
解得:m=1或m=0,
∴P(1,4)或P(0,3).
②当P点在x轴下方时,过P点作PM垂直于l于M点,过B点作BN垂直于MP的延长线与N点,
同理可得△PQM≌△BPN,
∴PM=BN,
∴PM=6﹣(3﹣m)=3+m,BN=m2﹣2m﹣3,
则3+m=m2﹣2m﹣3,
解得m= ![]() 或
或 ![]() .
.
∴P( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
综上可得,符合条件的点P的坐标是(1,4),(0,3),( ![]() ,
, ![]() )和(
)和( ![]() ,
, ![]() ).
).
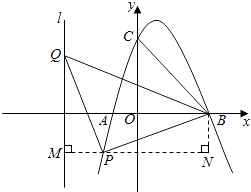
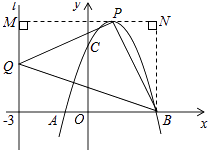
【解析】(1)利用待定系数法求出抛物线的解析式即可;(2)先求出直线BC解析式为y=﹣x+3,再求出抛物线顶点坐标,得出当x=1时,y=2;结合抛物线顶点坐即可得出结果;(3)设P(m,﹣m2+2m+3),Q(﹣3,n),由勾股定理得出PB2=(m﹣3)2+(﹣m2+2m+3)2 , PQ2=(m+3)2+(﹣m2+2m+3﹣n)2 , BQ2=n2+36,过P点作PM垂直于y轴,交y轴与M点,过B点作BN垂直于MP的延长线于N点,由AAS证明△PQM≌△BPN,得出MQ=NP,PM=BN,则MQ=﹣m2+2m+3﹣n,PN=3﹣m,得出方程﹣m2+2m+3﹣n=3﹣m,解方程即可.本题是二次函数综合题目,考查了用待定系数法求出抛物线的解析式、抛物线的顶点式、等腰直角三角形的性质、全等三角形的判定与性质、坐标与图形性质等知识;本题综合性强,有一定难度,特别是(3)中,需要通过作辅助线证明三角形全等才能得出结果.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.
-
科目: 来源: 题型:
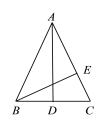
查看答案和解析>>【题目】在三角形ABC中,AB=AC,D是底边上的中点,BE垂直AC于点E,①∠ABC=∠ACB;②AD⊥BC;③∠BAD=∠CBE;④AB=2BD,其中正确的有___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过D作DE⊥AC于E,AB-BC=4,AC=8,则△ABP面积为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=
 .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数
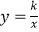 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( ) 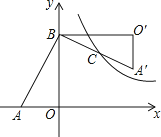
A.3
B.4
C.6
D.8 -
科目: 来源: 题型:
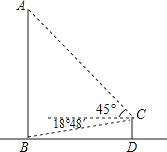
查看答案和解析>>【题目】全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为米(参考数据:tan78°12′≈4.8).
相关试题

