【题目】已知OABC的顶点A、C分别在直线x=2和x=4上,O为坐标原点,直线x=2分别与x轴和OC边交于D、E,直线x=4分别与x轴和AB边的交于点F、G.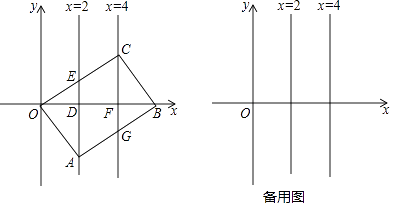
(1)如图,在点A、C移动的过程中,若点B在x轴上,
①直线 AC是否会经过一个定点,若是,请直接写出定点的坐标;若否,请说明理由.
②OABC是否可以形成矩形?如果可以,请求出矩形OABC的面积;若否,请说明理由.
③四边形AECG是否可以形成菱形?如果可以,请求出菱形AECG的面积;若否,请说明理由.
(2)在点A、C移动的过程中,若点B不在x轴上,且当OABC为正方形时,直接写出点C的坐标.
参考答案:
【答案】
(1)
解:①是,经过定点(3,0).理由如下:
如图1中,连接AC交OB于K.
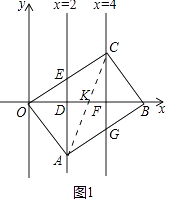
∵四边形OABC是平行四边形,
∴OK=KB,BC∥OA,BC=OA,
∴∠CBF=∠AOD,
在△DOA和△FBC中,
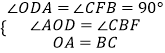 ,
,
∴△DOA≌△FBC,
∴OD=FB=2,
∴OB=6,
∵OK=KB,
∴OK=3,
∴K(3,0),
∴直线AC经过定点K(3,0).
②可以.利用如下:
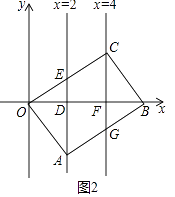
当∠OCB=90°时,四边形OABC是矩形,
由(1)可知△DOA≌△FBC,
∴OD=BF=2,
∵∠OCF+∠FCB=90°,∠FCB+∠CBF=90°,
∴∠OCF=∠CBF,
∵∠CFO=∠CFB,
∴△CFO∽△BFC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CF=2 ![]() ,
,
∴S矩形OABC=2S△OBC=2× ![]() ×
× ![]() =12
=12 ![]() .
.
③可以.理由如下:
如图3中,易知当OE=EC=AE时,四边形AECG是菱形.
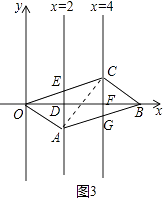
由(1)可知,△DOA≌△FBC,
∴AD=CF,
∵DE= ![]() CF,设DE=x,则AD=CF=2x,OE=AE=3x,
CF,设DE=x,则AD=CF=2x,OE=AE=3x,
在Rt△ADE中,∵OE2=OD2+DE2,
∴9x2=x2+4,
∴x= ![]() ,
,
∴AE= ![]() ,
,
∴S菱形AECG=AEDF= ![]() ×2=3
×2=3 ![]()
(2)
解:如图4中,
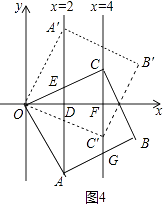
当四边形OABC是正方形时,易证△DOA≌△FCO,
∴OD=CF=2,
∴点C坐标(4,2),
根据对称性C′(4,﹣2)时,也满足条件.
综上所述,点C坐标为(4,2)或(4,﹣2)
【解析】(1)①是,经过定点(3,0).如图1中,连接AC交OB于K,只要证明OD=FB=2,推出OB=6,即可解决问题.②当∠OCB=90°时,四边形OABC是矩形,由(1)可知△DOA≌△FBC,推出OD=BF=2,由△CFO∽△BFC,可得 ![]() =
= ![]() ,由此即可解决问题.③可以.如图3中,易知当OE=EC=AE时,四边形AECG是菱形.由(1)可知,△DOA≌△FBC,推出AD=CF,易知DE=
,由此即可解决问题.③可以.如图3中,易知当OE=EC=AE时,四边形AECG是菱形.由(1)可知,△DOA≌△FBC,推出AD=CF,易知DE= ![]() CF,设DE=x,则AD=CF=2x,OE=AE=3x,在Rt△ADE中,根据OE2=OD2+DE2 , 列出方程即可解决问题.(2)如图4中,当四边形OABC是正方形时,易证△DOA≌△FCO,推出OD=CF=2,推出点C坐标(4,2),根据对称性C′(4,﹣2)时,也满足条件.
CF,设DE=x,则AD=CF=2x,OE=AE=3x,在Rt△ADE中,根据OE2=OD2+DE2 , 列出方程即可解决问题.(2)如图4中,当四边形OABC是正方形时,易证△DOA≌△FCO,推出OD=CF=2,推出点C坐标(4,2),根据对称性C′(4,﹣2)时,也满足条件.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半),还要掌握矩形的性质(矩形的四个角都是直角,矩形的对角线相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.

(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的 ⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求
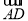 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
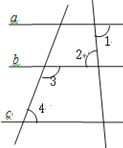
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,一次函数y=
 x+3的图象与y轴交于点A,点M在正比例函数y=
x+3的图象与y轴交于点A,点M在正比例函数y= x的图象x>0的那部分上,且MO=MA(O为坐标原点).
x的图象x>0的那部分上,且MO=MA(O为坐标原点).(1)求线段AM的长;
(2)若反比例函数y=
 的图象经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时,
的图象经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时,  x+3与
x+3与 的大小关系.
的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:
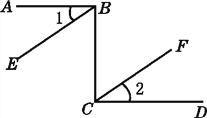
因为AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(______________),
所以∠ABC=∠BCD.
又因为∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF(______________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】枝江市2015年公共财政收入约为31.68亿元,对这个近似数而言,下列说法正确的是( )
A.精确到亿位
B.精确到百分位
C.精确到百万位
D.精确到千万位
相关试题

