【题目】探索题:
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律!

如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,就可以得到下面的等式:
(a+b)0=1.它只有一项,系数为1;
(a+b)1=a+b展开式中的系数1、1恰好对应图中第二行的数字;
(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;
(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.
(1)请认真观察此图,写出(a+b)4的展开式,(a+b)4= .
(2)类似地,请你探索并画出(a-b)0,(a-b)1,(a-b)2,(a-b)3的展开式中按a次数从大到小排列的项的系数对应的三角形.
(3)探究解决问题:求93+3×92+3×9+1 的值
参考答案:
【答案】(1)a4+4a3b+6a2b2+4ab3+b4;(2)详见解析;(3)1000
【解析】
(1)由已知条件可得![]() 的各项系数依次为1,4,6,4,1.
的各项系数依次为1,4,6,4,1.
(2)由已知式子可推出![]() 的系数是1,
的系数是1, ![]() 的系数是1和-1,以此类推可得出后面的式子.
的系数是1和-1,以此类推可得出后面的式子.
(3)根据式子可知满足![]() ,带入求解即可.
,带入求解即可.
(1)根据已知条件可得![]() .
.
(2)由题可得:
![]() 的系数是1,
的系数是1,
![]() 的系数是1和-1,
的系数是1和-1,
![]() 的系数是1,-2和1,
的系数是1,-2和1,
![]() 的系数是1,-3,3和-1,
的系数是1,-3,3和-1,
可得如下排列:
 .
.
(3) 原式=(9+1)3=1000.
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
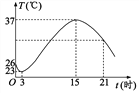
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:某校一块长为2a米的正方形空地是七年级四个班的清洁区,其中分给七年级(1)班的清洁区是一块边长为(a-2b)米的正方形,(0<b<
 ).
).(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y=
 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“丰收1号”小麦的试验田是边长为
 米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(
米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为( )米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
)米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则
 的值等于 .
的值等于 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生的艺术特长发展情况,某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.请你根据统计图解答下列问题:

(1)在这次调查中,一共抽查了名学生,其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 . 扇形统计图中喜欢“戏曲”部分扇形的圆心角为度.
(2)请你补全条形统计图.
(3)若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率.
相关试题

