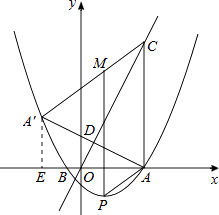
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;
x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;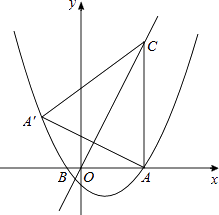
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵y= ![]() x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,
x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,
∴ 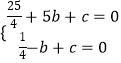 ,
,
解得 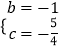 .
.
∴抛物线的解析式为y= ![]() x2﹣x﹣
x2﹣x﹣ ![]()
(2)
解:如答图所示,过点A′作A′E⊥x轴于E,AA′与OC交于点D,
∵点C在直线y=2x上,
∴C(5,10)
∵点A和A′关于直线y=2x对称,
∴OC⊥AA′,A′D=AD.
∵OA=5,AC=10,
∴OC= ![]() =
= ![]() =
= ![]() .
.
∵S△OAC= ![]() OCAD=
OCAD= ![]() OAAC,
OAAC,
∴AD= ![]() .
.
∴AA′= ![]() ,
,
在Rt△A′EA和Rt△OAC中,
∵∠A′AE+∠A′AC=90°,
∠ACD+∠A′AC=90°,
∴∠A′AE=∠ACD.
又∵∠A′EA=∠OAC=90°,
∴Rt△A′EA∽Rt△OAC.
∴ ![]() ,
,
即 ![]() .
.
∴A′E=4,AE=8.
∴OE=AE﹣OA=3.
∴点A′的坐标为(﹣3,4),
当x=﹣3时,
y= ![]() ×(﹣3)2+3﹣
×(﹣3)2+3﹣ ![]() =4.
=4.
所以,点A′在该抛物线上
(3)
解:存在.
理由:设直线CA′的解析式为y=kx+b,
则 ![]() ,
,
解得 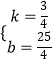
∴直线CA′的解析式为y= ![]() x+
x+ ![]()
设点P的坐标为(x, ![]() x2﹣x﹣
x2﹣x﹣ ![]() ),则点M为(x,
),则点M为(x, ![]() x+
x+ ![]() ).
).
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴( ![]() x+
x+ ![]() )﹣(
)﹣( ![]() x2﹣x﹣
x2﹣x﹣ ![]() )=10.
)=10.
解得x1=2,x2=5(不合题意,舍去)
当x=2时,y=﹣ ![]() .
.
∴当点P运动到(2,﹣ ![]() )时,四边形PACM是平行四边形
)时,四边形PACM是平行四边形
【解析】方法一:(1)利用待定系数法求出抛物线的解析式;(2)首先求出对称点A′的坐标,然后代入抛物线解析式,即可判定点A′是否在抛物线上.本问关键在于求出A′的坐标.如答图所示,作辅助线,构造一对相似三角形Rt△A′EA∽Rt△OAC,利用相似关系、对称性质、勾股定理,求出对称点A′的坐标;(3)本问为存在型问题.解题要点是利用平行四边形的定义,列出代数关系式求解.如答图所示,平行四边形的对边平行且相等,因此PM=AC=10;利用含未知数的代数式表示出PM的长度,然后列方程求解.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强用8 个边长不全相等的正三角形拼成如图所示的图案,其中阴影部分是边长为1 cm的正三角形.试求出图中正三角形A、正三角形B的边长分别是多少厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】温州苍南马站四季柚,声名远播,今年又是一个丰收年,某经销商为了打开销路,对1 000个四季柚进行打包优惠出售.打包方式及售价如图所示.假设用这两种打包方式恰好装完全部柚子.
(1)若销售a箱纸盒装和a袋编织袋装四季柚的收入共950元,求a的值;
(2)当销售总收入为7 280元时:
①若这批四季柚全部售完,请问纸盒装共包装了多少箱,编织袋装共包装了多少袋.
②若该经销商留下b(b>0)箱纸盒装送人,其余柚子全部售出,求b的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择.为了估计全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
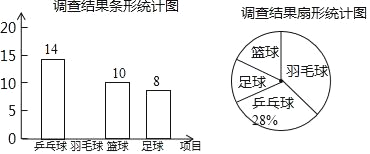
(1)求参加这次调查的学生人数,并补全条形统计图;
(2)求扇形统计图中“篮球”项目所对应扇形的圆心角度数;
(3)若该校共有600名学生,试估计该校选择“足球”项目的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是( )
A.“打开电视机,正在播NBA篮球赛”是必然条件
B.“掷一枚硬币正面朝上的概率是 ”表示每掷硬币2次就必有1次反面朝上.
”表示每掷硬币2次就必有1次反面朝上.
C.一组数据2,3,4,5,5,6的众数和中位数都是5
D.若甲组数据的方差S甲2=0.24,乙组数据的方差S乙2=0.03,则乙组数据比甲组数据稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC中,∠C=90°.
(1)若a=5,b=12,则c=________;
(2)若a=6,c=10,则b=_______;
(3)若a∶b=3∶4,c=10,则a=_______,b=_______.
-
科目: 来源: 题型:
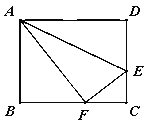
查看答案和解析>>【题目】折叠矩形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
相关试题

