【题目】如图(甲)是四边形纸片 ABCD,其中∠B=130°,∠D=50°.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C=_____.

参考答案:
【答案】90°
【解析】
根据两直线平行,同旁内角互补求出∠BPC和∠DRC,再根据翻折的性质求出∠CPR和∠CRP,然后利用三角形的内角和定理列式计算即可得解.
∵CP∥AB,RC∥AD,
∴∠BPC=180°-∠B=180°-130°=50°,
∠DRC=180°-∠C=180°-50°=130°,
由翻折的性质,∠CPR=![]() (180°-∠BPC)=
(180°-∠BPC)=![]() (180°-50°)=65°,
(180°-50°)=65°,
∠CRP=![]() (180°-∠DRC)=
(180°-∠DRC)=![]() (180°-130°)=25°,
(180°-130°)=25°,
在△CPR中,∠C=180°-∠CPR-∠CRP=180°-65°-25°=90°.
故答案为:90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, P 是直线 l 外一点,点 A、B、C 在 l 上,且 PB l ,下列说法:① PA、PB、PC 这 3 条线段中, PB 最短;②点 P 到直线 l 的距离是线段 PB 的长;③线段 AB 的长是点 A 到 PB 的距离;④线段 PA 的长是点 P 到直线 l 的距离. 其中正确的是( )
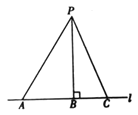
A. ①②③B. ①②④C. ①③④D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AB=10,BD=8,∠ACD=45°.
(1)求线段AD的长;
(2)求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )

A.9 B.10 C.3
 D.2
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连接AC,BC,作∠APC的平分线交AC于点D.
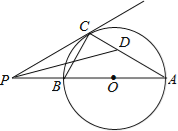
下列结论正确的是 (写出所有正确结论的序号)
①△CPD∽△DPA;
②若∠A=30°,则PC=
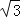 BC;
BC;③若∠CPA=30°,则PB=OB;
④无论点P在AB延长线上的位置如何变化,∠CDP为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知□ABCD的对角线AC与BD交于点O,求证:AB2+BC2+CD2+DA2=AC2+BD2.
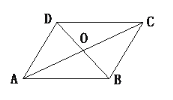
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
相关试题

