搜索
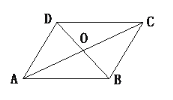
【题目】已知□ABCD的对角线AC与BD交于点O，求证：AB2+BC2+CD2+DA2=AC2+BD2.
参考答案：
【答案】证明见解析
【解析】
如图，过点O、C分别作DE⊥AB，CF⊥AB，E、F为垂足，运用勾股定理求证即可.
如图，过点O、C分别作DE⊥AB，CF⊥AB，E、F为垂足
又四边形ABCD是平行四边形
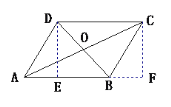
∴△ADE≌△BCF
∴AE=BF AB=EF=CD
∴AD2+BC2=AE2+DE2+BF2+CF2
AC2+BD2=AF2+CF2+DE2+BE2
=(AB+BF)2+CF2+DE2+(AB－AE)2
=(AB+BF)2+CF2+DE2+(AB－BF)2
=2AB2+2BF2+CF2+DE2
=AB2+CD2+BF2+AE2+CF2+DE2
=AB2+CD2+AD2+BC2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AD平行BC，∠ABC=90°，AD=2，AB=6，以AB为直径的半⊙O 切CD于点E，F为弧BE上一动点，过F点的直线MN为半⊙O的切线，MN交BC于M，交CD于N，则△MCN的周长为（ ）
A.9 B.10 C.3
D.2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（甲）是四边形纸片 ABCD，其中∠B＝130°，∠D＝50°.若将其右下角向内折出△PCR，恰使CP∥AB，RC∥AD，如图（乙）所示，则∠C＝_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】 如图，AB是⊙O的直径，P为AB延长线上的一个动点，过点P作⊙O的切线，切点为C，连接AC，BC，作∠APC的平分线交AC于点D．
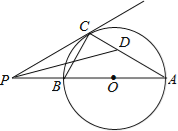
下列结论正确的是 （写出所有正确结论的序号）
①△CPD∽△DPA；
②若∠A=30°，则PC=
BC；③若∠CPA=30°，则PB=OB；
④无论点P在AB延长线上的位置如何变化，∠CDP为定值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A，B，C都在格点上．将△ABC绕点A按顺时针方向旋转90°得到△AB′C′．
（1）在正方形网格中，画出△AB′C′；
（2）计算线段AB在变换到AB′的过程中扫过的区域的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在⊙O中，直径AB＝6，BC是弦，∠ABC＝30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．
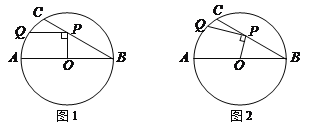
（1）如图1，当PQ∥AB时，求PQ的长度；
（2）如图2，当点P在BC上移动时，求PQ长的最大值．
-
科目： 来源： 题型：
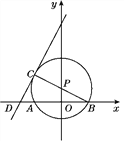
查看答案和解析>>【题目】如图，点P在y轴上，⊙P交x轴于A，B两点，连接BP并延长交⊙P于点C，过点C的直线y＝2x＋b交x轴于点D，且⊙P的半径为
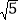，AB＝4.(1)求点B，P，C的坐标；
(2)求证：CD是⊙P的切线．
相关试题
