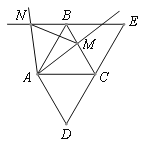
【题目】已知,如图,将∠D=60°的菱形ABCD沿对角线AC剪开,将△ADC沿射线DC方向平移,得到△BCE. 点M为BC边上一点(点M不与点B、点C重合),将射线AM绕点A逆时针旋转60°,与EB的延长线交于点N,连接MN.
(1)求证:∠ANB=∠AMC;
(2)探究△AMN的形状,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)①先由菱形可知四边相等,再由∠D=60°得等边△ADC和等边△ABC,则对角线AC与四边都相等,利用ASA证明△ANB≌△AMC,得结论;
②根据有一个角是60°的等腰三角形是等边三角形得出:△AMN是等边三角形;
试题解析:(1)∵ABCD为菱形,
∴AB=AD=CD=BC,
又∵∠D=60°,
∴△ADC为等边三角形,
∴∠DAC=60°,AC=AD,
∴AC=AB=BC,
又∵△BCE≌△ADC,∠CBE=∠DAC=60°,
∴∠CBN=120°
∵∠ANB=360°-∠CBN-∠MAN-∠BMA=180°-∠BMA,∠AMC=180°-∠BMA
∴∠ANB=∠AMC.
(2)∵AC=AB=BC,
∴△ABC为等边三角形,
∴∠BAC=60°.
∵∠MAN=60°,
∴∠MAN=∠BAC,
∴∠MAN-∠BAM=∠BAC-∠BAM,即∠BAN=∠CAM,
又∵∠ANB=∠AMC,AB=AC,
∴△BAN≌△CAM,
∴AN=AM,
∵∠MAN=60°,
∴△AMN为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )
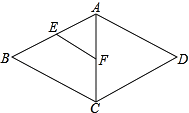
A.12
B.16
C.20
D.24 -
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
(1)一个角的余角与这个角的补角的和比平角的 多1°,求这个角的度数.
多1°,求这个角的度数.
(2)已知5m=2,5n=3,求53m﹣2n . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
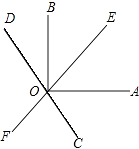
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数.(用含α的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】以下条件不能判别四边形ABCD是矩形的是( )
A.AB=CD,AD=BC,∠A=90°
B.OA=OB=OC=OD
C.AB=CD,AB∥CD,AC=BD
D.AB=CD,AB∥CD,OA=OC,OB=OD -
科目: 来源: 题型:
查看答案和解析>>【题目】某开发区去年出口创汇额为25亿美元,今年达到30.55亿美元,已知今年上半年出口创汇额比去年同期增长18%,下半年比去年同期增长25%,求去年上半年和下半年的出口创汇额各是多少亿美元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
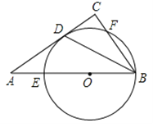
(1) 求证:AC是⊙O的切线;
(2) 已知AB=10,BC=6,求⊙O的半径r.
相关试题

