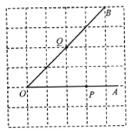
【题目】如图,点P,Q分别是∠AOB的边OA,OB上的点.
(1)过点P画OB的垂线,垂足为H;
(2)过点Q画OA的垂线,交OA于点C,连接PQ;
(3)线段QC的长度是点Q到 的距离, 的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是 (用“<”号连接).
参考答案:
【答案】(1)画图见解析;(2)见解析;(3)直线OA,线段PH;PH<PQ.
【解析】
(1)根据垂线的概念、结合网格特点作图即可;(2)根据垂线的概念、结合网格特点和线段的作法作图;(3)根据垂线段最短进行比较即可.
(1)如图,直线PH即为所求;
(2)如图,直线QC即为所求;
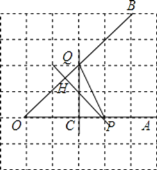
(3)线段QC的长度是点Q到直线OA的距离,线段PH的长度是点P到直线OB的距离,
根据直线外一点和直线上各点连接的所有线段中,垂线段最短可知PH<PQ,
故答案为:直线OA,线段PH;PH<PQ.
-
科目: 来源: 题型:
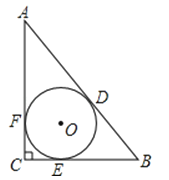
查看答案和解析>>【题目】如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
(1)一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)=
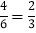 .
.(2)口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)=
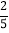 .
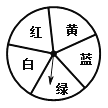
.(3)如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)=
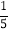 .
.问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现场学习:
在一次数学兴趣小组活动中,老师和几个同学一起探讨:在an=b中,a,b,n三者关系.
同学甲:已知a,n,可以求b,是我们学过的乘方运算,其中b叫做a的n次方.如:(﹣2)3=﹣8,其中﹣8是﹣2的3次方.
同学乙:已知b,n,可以求a,是我们学过的开方运算,其中a叫做b的n次方根.如:(±2)2=4,其中±2 是4的二次方根(或平方根);(﹣3)3=﹣27,其中﹣3是﹣27的三次方根(或立方根).
老师:两位同学说的很好,那么请大家计算:
(1)81的四次方根等于 ;﹣32的五次方根等于 .
同学丙:老师,如果已知a和b,那么如何求n呢?又是一种什么运算呢?
老师:这个问题问的好,已知a,b,可以求n,它是一种新的运算,称为对数运算.
这种运算的定义是:若an=b(a>0,a≠1),n叫做以a为底b的对数,记作:n=logab.例如:23=8,3叫做 以2为底8的对数,记作3=log28.根据题意,请大家计算:
(2)log327= ; (
 )﹣2+
)﹣2+ ﹣log4
﹣log4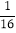 = .
= .随后,老师和同学们又一起探究出对数运算的一条性质:如果a>0,a≠1,M>0,N>0,那么logaMN=logaM+logaN.
(3)请你利用上述性质计算:log53+log5
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC,∠B=70°,∠C=30°.求:
(1)∠BAE的度数;
(2)∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算a
 b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:①2
 (-2)=6 ②a
(-2)=6 ②a b=b
b=b a
a③若a+b=0,则(a
 a)+(b
a)+(b b)=2ab ④若a
b)=2ab ④若a b=0,则a=0.
b=0,则a=0.其中正确结论的序号是 (填上你认为所有正确结论的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边长a=3,b=4,c=5,则它的内切圆半径是
相关试题

