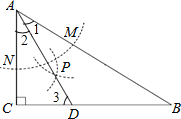
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
参考答案:
【答案】A
【解析】
试题分析:①根据作图的过程可以判定AD是∠BAC的角平分线;
②利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
③利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上;
④根据直角三角形的性质得出AD=2CD,再由线段垂直平分线的性质得出AD=BD,进而可得出结论.
解:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°﹣∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
∵∠2=30°,
∴AD=2CD.
∵点D在AB的中垂线上,
∴AD=BD,
∴BD=2CD.
故④正确.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.
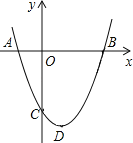
(1)求该抛物线的函数关系式;
(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD,请求出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)
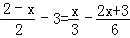 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市5年前人均年收入为n元,预计今年人均年收入是5年前的2倍多800元,则今
年人均年收入将达____ _____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工作组,甲组有25人,乙组有17人,若从乙组调x人到甲组,那么甲组的人数恰好是乙组人数的2倍,依据题意可列出方程 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,Rt△ABC中,∠ACB=90°,AC=BC,∠ABC的角平分线交AC于E,AD⊥BE于D,求证:AD=
 BE.
BE.
相关试题

