【题目】已知,Rt△ABC中,∠ACB=90°,AC=BC,∠ABC的角平分线交AC于E,AD⊥BE于D,求证:AD=![]() BE.
BE.

参考答案:
【答案】见解析
【解析】
试题分析:延长AD和BC交于F,求出∠CBE=∠CAF,AC=BC,证△EBC≌△FAC,△ABD≌△FBD,推出BE=AF,AD=DF,即可得出答案.
解:如图延长AD和BC交于F,

∵Rt△ABC中,∠ACB=90°,∠BAC=45°,
∴∠ABC=45°=∠BAC,
∴AC=BC,
∵∠ACB=90°,
∴∠BCE=∠ACF=90°,
∵BE平分∠ABC,
∴∠ABD=∠EBC,
∵BD⊥AD,
∴∠BCE=∠ADE=90°,
∵∠BEC=∠AED,
∴根据三角形内角和定理得:∠DAE=∠CBE,
在△BCE和△ACF中,
 ,
,
∴△BCE≌△ACF(SAS),
∴BE=AF,
在△ABD和△FBD中,
 ,
,
∴△ABD≌△FBD(ASA),
∴AD=DF,
即AF=2AD,
∴AD=![]() AF,
AF,
∴AD=![]() BE.
BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市5年前人均年收入为n元,预计今年人均年收入是5年前的2倍多800元,则今
年人均年收入将达____ _____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工作组,甲组有25人,乙组有17人,若从乙组调x人到甲组,那么甲组的人数恰好是乙组人数的2倍,依据题意可列出方程 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具店用2000元购进一批玩具,面市后,供不应求,于是店主又购进同样的玩具,所购的数量是第一批数量的3倍,但进价贵了4元,结果购进第二批玩具共用了6300元,若两批玩具的售价都是120元,且两批玩具全部售完,求该玩具店销售这两批玩具共盈利多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .

-
科目: 来源: 题型:
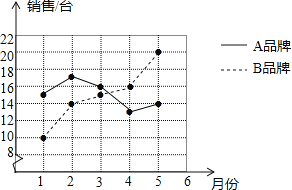
查看答案和解析>>【题目】某商场统计了今年1﹣5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:
(1)根据图中数据填写表格.

(2)通过计算该商场这段时间内A、B两种品牌冰箱月销售量的方差,比较这两种品牌冰箱月销售量的稳定性.
相关试题

