【题目】如图1,已知直线l1∥l2 , 且l1、l2分别相交于A、B两点,l4和l1、l2分别交于C、D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3.点P在线段AB上. 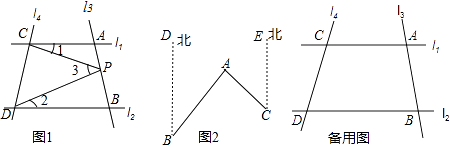
(1)若∠1=22°,∠2=33°,则∠3= .
(2)试找出∠1、∠2、∠3之间的等量关系,并说明理由.
(3)应用(2)中的结论解答下列问题: 如图2,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数.
(4)如果点P在直线l3上且在A、B两点外侧运动时,其他条件不变,试探究∠1、∠2、∠3之间的关系(点P和A、B两点不重合),直接写出结论即可.
参考答案:
【答案】
(1)55°
(2)解:∠1+∠2=∠3,
∵l1∥l2,
∴∠1+∠PCD+∠PDC+∠2=180°,
在△PCD中,∠3+∠PCD+∠PDC=180°,
∴∠1+∠2=∠3

(3)解:过A点作AF∥BD,则AF∥BD∥CE,则∠BAC=∠DBA+∠ACE=40°+45°=85°
(4)解:当P点在A的外侧时,如图2,
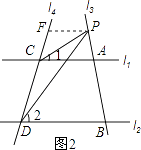
过P作PF∥l1,交l4于F,
∴∠1=∠FPC.
∵l1∥l4,
∴PF∥l2,
∴∠2=∠FPD
∵∠CPD=∠FPD﹣∠FPC
∴∠CPD=∠2﹣∠1.
当P点在B的外侧时,如图3,
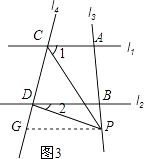
过P作PG∥l2,交l4于G,
∴∠2=∠GPD
∵l1∥l2,
∴PG∥l1,
∴∠1=∠CPG
∵∠CPD=∠CPG﹣∠GPD
∴∠CPD=∠1﹣∠2.
【解析】解:(1)∠1+∠2=∠3. ∵l1∥l2 ,
∴∠1+∠PCD+∠PDC+∠2=180°,
在△PCD中,∠3+∠PCD+∠PDC=180°,
∴∠3=∠1+∠2=55°,
所以答案是:55°;
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC绕一点旋转到△A′B′C′,则△ABC和△A′B′C′的关系是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,0)、B(b,0),且(a+4)2+|b﹣2|=0.

(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的 ?若存在,求出点D的坐标;若不存在,请说明理由.
?若存在,求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】生活中,有时也用“千千万”来形容数量多,“千千万”就是100亿,“千千万”用科学记数法可表示为( )
A. 0.1×1011B. 10×109C. 1×1010D. 1×1011
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形ABCO绕点A顺时针旋转一定角度,得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)若正方形ABCO的边长为
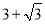 ,∠1=∠2,求AP的长.
,∠1=∠2,求AP的长.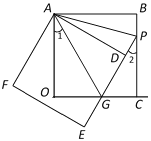
-
科目: 来源: 题型:
查看答案和解析>>【题目】河流两岸a、b互相平行,C、D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值(结果精确到个位).
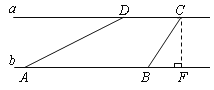
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果等式(x﹣3)2x﹣1=1,则x= .
相关试题

