【题目】如图,在平面直角坐标系中,已知抛物线y=a(x-5)(x+1)与x轴交于点A,B两点,与y轴交于点C(0,![]() ).
).
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF.当线段EF的长度最短时,求出点G的坐标.

参考答案:
【答案】(1)![]() ;(2)P(-5,-20);(3)G(
;(2)P(-5,-20);(3)G(![]() ,2) (
,2) (![]() ,2)
,2)
【解析】试题分析:(1)运用待定系数法即可求出抛物线的解析式;
(2)过点A作![]() ,交
,交![]() 轴于点
轴于点![]() ,交抛物线与点
,交抛物线与点![]() ,通过
,通过![]() ∽
∽![]() 求得OH的长,从而得到H点坐标,继而得到直线AP的解析式,与抛物线解析式联立即可得到点P坐标;
求得OH的长,从而得到H点坐标,继而得到直线AP的解析式,与抛物线解析式联立即可得到点P坐标;
(3)连接OD,易得四边形OFDE是矩形,则OD=EF,根据垂线段最短可得当![]() 时,OD(即EF)的长度最小.然后只需求出点D的纵坐标,就可得到点G的纵坐标,代入解析式就可求出点G的横坐标,从而得到点G的坐标.
时,OD(即EF)的长度最小.然后只需求出点D的纵坐标,就可得到点G的纵坐标,代入解析式就可求出点G的横坐标,从而得到点G的坐标.
(1) ∵抛物线![]() 与
与![]() 轴交于点C(0,
轴交于点C(0, ![]() ),∴
),∴![]() ,
,
∴![]() ;
;
(2)过点A作![]() ,交
,交![]() 轴于点
轴于点![]() ,交抛物线与点
,交抛物线与点![]() ,则A(5,0),B(-1,0)
,则A(5,0),B(-1,0)
∵![]() ,
, ![]()
∴![]() ∽
∽![]() span> ∴
span> ∴![]() ∴
∴![]() ;
;
又∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∴H(0,-10),A(5,0),∴直线AP的解析式为y=2x-10![]() ,
,
联立 ∴P(-5,-20);
∴P(-5,-20);
(3)∵![]() 轴,
轴, ![]() 轴,∴四边形OFDE是矩形,∴EF=OD,
轴,∴四边形OFDE是矩形,∴EF=OD,
∴EF长度的最小值为OD长度的最小值,当![]() 时,OD的长度最小.
时,OD的长度最小.
此时![]() ,
, ![]() ,
, ![]()
又∵![]() 轴,
轴, ![]() ,∴
,∴![]() ∽
∽![]() ,∴
,∴![]()
∴![]() ,∴OE=2,∴点G的纵坐标为2,
,∴OE=2,∴点G的纵坐标为2,
∴![]() 解得
解得![]() ,
, ![]()
∴G(![]() ,2) (
,2) (![]() ,2).
,2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)综合素质
考试成绩
体育测试
满分
100
100
100
小聪
72
98
60
小亮
90
75
95
调查二:对九年级(2)班50名同学某项跑步成绩进行调查,并绘制了一个不完整的扇形统计图,请你根据以上提供的信息,解答下列问题:
(1)小聪和小亮谁能达到“优秀毕业生”水平?哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议.
(3)扇形统计图中“优秀率”是多少?
(4)“不及格”在扇形统计图中所占的圆心角是多少度?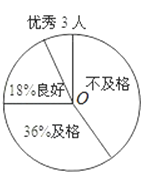
-
科目: 来源: 题型:
查看答案和解析>>【题目】某渔场计划购买甲、乙两种鱼苗共6000尾,甲种鱼苗每尾0.5元,乙种鱼苗每尾0.8元.相关资料表明:甲、乙两种鱼苗的成活率分别为90%和95%.
(1)若购买这批鱼苗共用了3600元,求甲、乙两种鱼苗各购买了多少尾?
(2)若要使这批鱼苗的成活率不低于93%,且购买鱼苗的总费用最低,应如何选购鱼苗? -
科目: 来源: 题型:
查看答案和解析>>【题目】经过一点A画已知直线a的平行线,能画( )
A. 0条 B. 1条 C. 2条 D. 0条或1条
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形,正三角形,等腰梯形和菱形四种图形,你认为符合条件的是( )
A.等腰三角形
B.正三角形
C.等腰梯形
D.菱形 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(﹣3,2)关于原点对称的点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.

相关试题

