【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
参考答案:
【答案】(1)A、B两种净水器的销售单价分别为2500元、2100元;(2)超市最多采购A种型号净水器10台时,采购金额不多于54000元;(3)采购A种型号净水器8台,采购B种型号净水器22台,公司能实现利润12800元的目标.
【解析】设A、B两种净水器的销售单价分别为x元,y元,
由题意得:![]()
答:A、B两种净水器的销售单价分别为2500元,2100元.
设采购A种型号的净水器a台,则B种净水器(30—a)台.
由题意得:2000a+1700(30-a)![]()
解得:![]()
故超市最多采购A种型号净水器10台,采购金额不多于54000元.
由题意得:![]()
解得a=8,
故采购A种型号净水器8台,B种型号净水器22台,公司能实现12800元的目标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
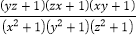 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=2x-7平移后的图象l经过点(-3,-2),
(1)求l的函数解析式;并画出该函数的图象;
(2)l与x轴交于点A,点P是l上一点,且S△AOP=
 ,求点P的坐标.
,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α+β=1,αβ=﹣1.设S1=α+β,S2=α2+β2,S3=α3+β3,…,Sn=αn+βn,
(1)计算:S1= ,S2= ,S3= ,S4= ;
(2)试写出Sn﹣2、Sn﹣1、Sn三者之间的关系;
(3)根据以上得出结论计算:α7+β7.
-
科目: 来源: 题型:
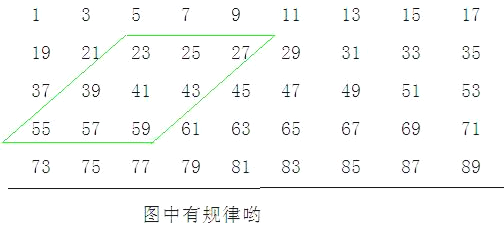
查看答案和解析>>【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料: 1×2=
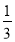 (1×2×3-0×1×2),2×3=
(1×2×3-0×1×2),2×3=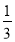 (2×3×4-1×2×3),3×4=
(2×3×4-1×2×3),3×4=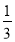 (3×4×5- 2×3×4),
(3×4×5- 2×3×4),由以上三个等式左、右两边分别相加,可得:
1×2+2×3+3×4=
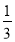 ×3×4×5=20
×3×4×5=20 读完以上材料,请你计算下列各题(写出过程):
(1)1×2+2×3+3×4+…+10×11= ;
(2)1×2+2×3+3×4+…+n×(n+1)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(规律探索)如图所示的是由相同的小正方形组成的图形,每个图形的小正方形个数为Sn,n是正整数.观察下列图形与等式之间的关系.
第一组:
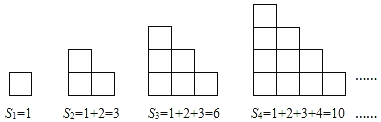
第二组:
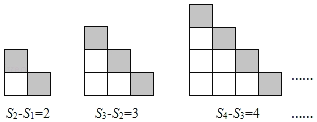
第三组:
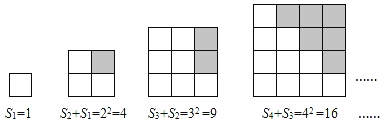
(规律归纳)
(1)S7﹣S6= ;Sn﹣Sn﹣1= .
(2)S7+S6= ;Sn+Sn﹣1= .
(规律应用)
(3)计算
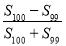 的结果为 .
的结果为 .
相关试题

