【题目】如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠a.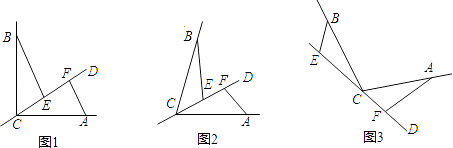
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图l,若∠BCA=90°,∠a=90°,则BECF;EF|BE﹣AF|(填“>”,“<”或“=”);
②如图(2),若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 , 使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
参考答案:
【答案】
(1)=;=;∠α+∠BCA=180°
(2)
解:EF=BE+AF.
理由是:如图3中,
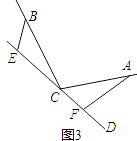
∵∠BEC=∠CFA=∠a,∠a=∠BCA,
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,
∴∠EBC+∠BCE=∠BCE+∠ACF,
∴∠EBC=∠ACF,
在△BEC和△CFA中,
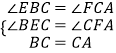 ,
,
∴△BEC≌△CFA(AAS),
∴AF=CE,BE=CF,
∵EF=CE+CF,
∴EF=BE+AF
【解析】解:(1)①如图1中,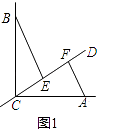
E点在F点的左侧,
∵BE⊥CD,AF⊥CD,∠ACB=90°,
∴∠BEC=∠AFC=90°,
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,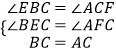 ,
,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=CF﹣CE=BE﹣AF,
当E在F的右侧时,同理可证EF=AF﹣BE,
∴EF=|BE﹣AF|;
所以答案是=,=.
②∠α+∠ACB=180°时,①中两个结论仍然成立;
证明:如图2中,
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,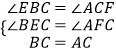 ,
,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=CF﹣CE=BE﹣AF,
当E在F的右侧时,同理可证EF=AF﹣BE,
∴EF=|BE﹣AF|;
所以答案是∠α+∠ACB=180°.
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果线段AB=6,点C在直线AB上,BC=4,D是AC的中点,那么A、D两点间的距离是( )
A.5
B.2.5
C.5或2.5
D.5或1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的对称轴为直线
的对称轴为直线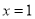 ,与
,与 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
①
 ;② 方程
;② 方程 的两个根是
的两个根是 ;③
;③ 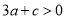 ;④当
;④当 时,
时,  的取值范围是
的取值范围是 ;⑤ 当
;⑤ 当 时,
时,  随
随 增大而增大;其中结论正确有____.
增大而增大;其中结论正确有____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形的边长为a,以各边才为直径在正方形内画半圆,所围成的图形(图中阴影部分)的面积为( )

A. a2﹣
a2﹣ 
B. ﹣a2
﹣a2
C.a2﹣
D.πa2﹣a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“太阳每天从东方升起”,这是一个_____________事件(填“确定”或“随机”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)先化简,再求值:(3x2﹣4)+(2x2+5x﹣6)﹣2(x2﹣5),其中x=﹣2
(2)解方程: ﹣
﹣ 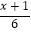 =2.
=2.
相关试题

